[科普中国]-面积原理

面积原理亦称格朗沃尔面积定理，是∑类函数展开式系数的一个性质定理。此定理由格朗沃尔(Gronwall , T. H.)于1915年提出。

简介面积原理亦称格朗沃尔面积定理，是∑类函数展开式系数的一个性质定理，此定理由格朗沃尔(Gronwall , T. H.)于1915年提出。

该定理断言：若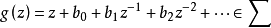 ，则 。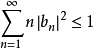

证明设w=u+iv=F(ζ)将圆周|ζ|=ρ（具有正向）映照成闭曲线Γρ，其内部区域面积为Sρ，则

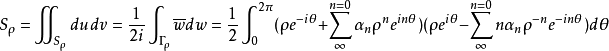
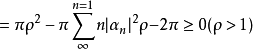令ρ→1即得定理的前半部分。

等号成立限于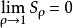 ，即得映像区域无外点。

应用之所以称其为面积原理，是因为定理的结论是根据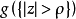 的余集的面积大于零的几何事实而得到的，这里ρ可以是任何大于1的数。

从格朗沃尔面积原理的证明可见，面积原理的内容是可以推广的，并由此可产生一系列美好的不等式，如格伦斯基不等式或戈鲁金不等式。1

∑类∑类是一类单叶函数。

它是由全体在单位圆外具有展开式g(z)=z+b0+b1z-1+b2z-2(1