[科普中国]-车多项式

车多项式(rook polynomials)是美国数学家John Riordan在研究国际象棋中车的禁位排列问题时创立的多项式。设B为n个对象受限制的排列问题的棋盘，rk(B)(k=1，2，…，n)是B的不同行不同列中取k个小暗方块的不同方法的数目，则称多项式R(x，B)=1+r1(B)x+r2(B)x2+…+rn(B)xn为B的车多项式1。

基本介绍车多项式是研究棋阵问题的主要工具，x的多项式

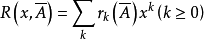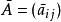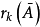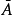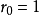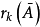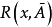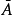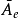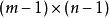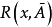称为以矩阵=(ij)为棋阵的车多项式，这里，表示k只车分布到与棋阵相应的棋盘B上的不同的分布数，约定，当k大于棋盘B上的可用格个数时，=0，于是，)是一个x的多项式，若在棋阵中任选一个可用格a，把该可用格换为禁用格而其他格不变所得的棋阵记为，把该可用格所在行和列都删去所得出的一个棋阵记为，则按棋阵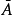之可用格a的展开式是

反复利用对可用格的展开式，可将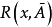的计算归纳为一些已知的或易算的车多项式的计算2。

相关定理下文设C是任一个棋盘，令

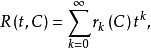则R(t，C)称为棋盘c的车多项式。

求棋盘车多项式的一般方法是：把求较大的棋盘的车多项式的问题转化成去求较小的棋盘的车多项式3。

为简便计，在不会引起误会的情况下，常把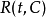简写成R(t)，把rk(C)简写成rk。

定理1 设a是棋盘C上的任一个格子，以C'a表示从C中去掉与a同行或同列的全部格子后所得的棋盘，以Ca表示从C中去掉格子a后所得的棋盘，则3

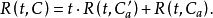
证明：个车在G上的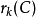种好布局可分成如下两类：

(1)有一个车放在a上的好布局，因为其余k-1个车放在C'a上，所以属于此类的好布局有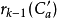种。

(2)没有车放在a上的好布局．因为k个车全部放在Ca上，所以属于此类的好布局有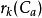种。

由加法原则，有

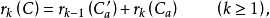所以

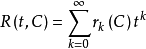
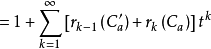
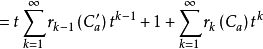
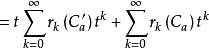
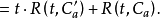
定理2 设C₁和C₂都是棋盘C的子棋盘，C由C₁和C₂拼成，且C₁和C₂彼此分离，即C₁中的任一格子与C₂中的任一格子在C上既不同行也不同列，则3

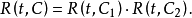
本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学