[科普中国]-布利萨德算法

布利萨德算法(Blissard's calculus)亦称哑运算，是一种特殊的符号演算法，它是英国数学家布利萨德(J.Blissard)创造的1。

基本介绍设数列{ak}，{bk}，{ck}(k=0，1，2…)的指数型生成函数分别为

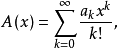
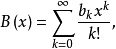
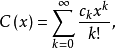
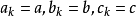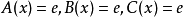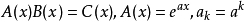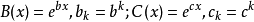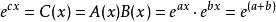若，则，按此算出结果后，再将相应指数移到下标位置，可以得出问题的真实答案，例如，将该算法用于指数型生成函数之积，若，，则，从而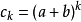，由此得出1

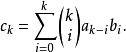
相关分析指数型发生函数不仅对研究排列问题是必要的，而且在计算概率统计中的矩量时也是极有用的工具，这里我们专来讨论指数型发生函数的运算性质，特别要介绍Blissard形式演算法则。

令数列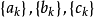相应的指数型发生函数分别记作

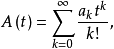
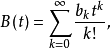
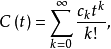则当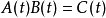时，由比较tk项系数可得下列等式：

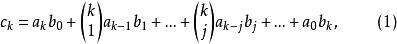这表明它和普通发生函数的数列卷积形式有所不同,但正因为其中出现了二项系数，且与二项展开式十分相似，便使人想到可将它按二项展开公式这样的形式来缩记。例如，我们可以纯粹作为形式符号来表记

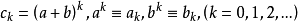
这就是说，在演算过程中可把足标移到指数地位来演算，但演算完毕之后，对最终结果仍须让指数返回足标位置,这种形式算法即称为Blissard演算或“哑演算”(umbral oalculas)．

上述哑演算的合理性本质上是基于指数型发生函数在作乘法运算与求导等演算时，能与哑演算法则一一对应起来，并使最终结果具有一致性,具体说来，按哑演算规定法则，可简记

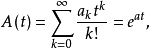
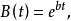
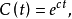其中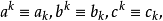又由形式演算得

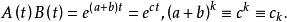其中ck恰好可由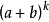进行哑演算面算出，这一段无非表明按哑演算进行乘法运算时最终结果是一定正确的。

对A(t)进行求导运算，可得

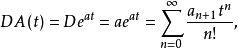
这表明哑演算仍继续得出正确结果．由上所论，至少已能看出，哑演算应用于形式指函数的乘法与求导，总是行之有效的，当然，乘法与求导运算可以反复进行2。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学