西蒙-纽科姆问题(Simon-Newcomb's problem)是确定某种排列数的一个问题,设π是多重集S={iki|i=1,2,…,n}的一个排列,把π分段,使得段数最少且每段中数字呈非降顺序,这样的每一段称为π的一个上升段.所谓西蒙-纽科姆问题就是求S的恰有r个上升段的排列数N(1k1,2k2,…,nkn;r).若以S2(n,k)表第二类斯特林数,则N(1k1,2k2,…,nkn;r)等于(A)k11(A)k22…(A)knn的展开式中xr的系数,其中的(A)i=A(A+1-x)(A+2-2x)…·(A+k-1-(k-1)x),Ai≡Ai(x),n=1,2,…,且Ai(x)=x∑i-1k=0S2(i,i-k)(i-k)!(x-1)k。1
基本介绍十九世纪著名的英国天文学家西蒙·纽科姆(Simon Newcomb)把一副扑克牌一张一张地放在桌上,只要牌的面值是以非减次序出现的,他就把它们堆成一堆,但每当待堆放的下一张牌的面值小于前者时,他就开始一个新的堆,他想要知道,在整副牌以这种方式分发完毕之后,形成给定堆数的概率。
因此,西蒙·纽科姆问题就是,求在一个多重集合的随机排列中,路段的概率分布问题2。
相关介绍下面将推导出现于这个游戏中的平均堆数2。
首先假定有m种不同类型的牌,每种类型恰有p张。例如,通常的桥牌,如果不考虑花色时,有m=13和p=4。P.A.麦克马洪发现了应用于这种情况的值得注意的对称性(Combinatory Analysis1,(Cambridge,1915),212-213]:有k+1个路段的排列个数等同于有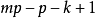 个路段的排列个数。当p=1时,这个关系易于验证,但对于p>1时,它是十分令人惊奇的。
个路段的排列个数。当p=1时,这个关系易于验证,但对于p>1时,它是十分令人惊奇的。
显然,没有很简单的对应;麦克马洪的证明是以生成函数而不是以一种组合构造为基础的。但福塔的对应提供了一个有用的简化,因为它告诉我们,在具有k-1个路段的排列和其两行表示法恰含有k个x1的情况,而且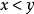 等价于
等价于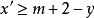 。由于(1)对应于具有南k+1个路段的一个排列,而(2)对应于具有
。由于(1)对应于具有南k+1个路段的一个排列,而(2)对应于具有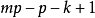 个路段的一个排列,而且由于把(1)变为(2)的变换是可逆的(它把(2)变回(1)],麦克马洪的对称性条件已经建立。
个路段的一个排列,而且由于把(1)变为(2)的变换是可逆的(它把(2)变回(1)],麦克马洪的对称性条件已经建立。
由于对称性,在一个随机排列中路段的平均数必须是
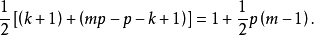 例如,利用一副标准扑克牌,由西蒙·纽康姆的单人游戏得到的平均堆数将是25(所以它不象是一种有吸引力的单人游戏)。
例如,利用一副标准扑克牌,由西蒙·纽康姆的单人游戏得到的平均堆数将是25(所以它不象是一种有吸引力的单人游戏)。
给定任意多重集合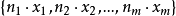 ,其中诸x是不同的,利用一个相当简单的论证,实际上可以一般地确定路段的平均数。设
,其中诸x是不同的,利用一个相当简单的论证,实际上可以一般地确定路段的平均数。设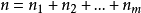 ,并想象这个多重集合的所有排列
,并想象这个多重集合的所有排列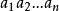 都已经写下来,我们来考察;对于每个固定的i值,
都已经写下来,我们来考察;对于每个固定的i值,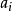 大于
大于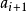 的机会如何,这里1≤i
的机会如何,这里1≤i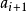 的次数恰是
的次数恰是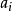 ≠
≠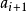 的次数之半,而且不难看出,
的次数之半,而且不难看出,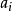 =
=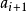 =xj恰有
=xj恰有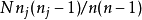 次,其中N是排列的总数。因此,
次,其中N是排列的总数。因此,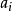 =
=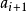 恰有:
恰有:
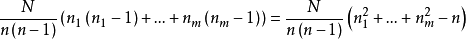 次,而且
次,而且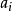 >
>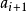 恰有
恰有
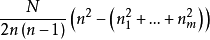 次。因为在每个排列中定有一个路段在an处结束,因此若对i求和并加上N,则得到在所有N个排列当中路段的总数
次。因为在每个排列中定有一个路段在an处结束,因此若对i求和并加上N,则得到在所有N个排列当中路段的总数
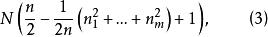 除以N即给出所求的平均路段数2。
除以N即给出所求的平均路段数2。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国