[科普中国]-布鲁克-赖瑟-乔拉定理

布鲁克-赖瑟-乔拉定理(Bruck-Ryser-Chowla theorem)是反映对称设计存在的必要条件的一个事实,若(v，k，λ)-SBIBD存在，记n=k-λ，则当v为偶数时，n为平方数;当v为奇数时，不定方程z²=nx²+(-1)(v-1)/2λy²有不全为零的整数解x，y，z，利用这个定理可以确定某些对称设计的不存在性，例如，因为22是偶数，而n=5不是平方数，所以(22，7，2)-SBIBD不存在。另外，这个定理给出的条件并不是充分的。例如，最近证明了10阶射影平面不存在，即(111，11，1)-SBIBD不存在1。

基本介绍布鲁克-赖瑟-乔拉定理(BRC定理) 令k-λ=n>o，若SB(k，λ；v)存在。则

(i) 当v为偶数时，n为平方数；

(ii) 当v为奇数时。不定方程

有不全为零的整数解x,y,z。

相关定理由定理1和定理2可证明布鲁克-赖瑟-乔拉定理，接下来的两引理也可证出布鲁克-赖瑟-乔拉定理。以下所有定理的证明以及布鲁克-赖瑟-乔拉定理的证明请参考相应文献2。

关于B(k，λ；v)存在性的必要条件，在对称设计的情形，由于b=v，因此化为

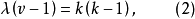即

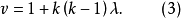
对称性的要求是一个很强的限制条件。因此对于很多满足条件(1)的参数v,k,λ,SB(k，λ；v)并不存在。下述定理即说明了这点。

定理1 设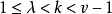，令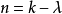,若SB(k，λ；v)存在。则

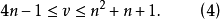
由定理1可知。对任一给定的正整数n及所有满足条件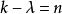的正整数对k,λ。使SB(k，λ；v)存在的正整数v只有有限多个。

本节主要目的在证明关于对称设计存在性的一个重要定理。即著名的Bruck-Ryser-Chowla定理(BRC定理)，为此还要用到数论中的下述结果。

定理2 (Lagrange四平方和定理)任一正整数n都能表成4个整数的平方和：

由以上引理可证明布鲁克-赖瑟-乔拉定理，下面两引理也可证出布鲁克-赖瑟-乔拉定理。

引理1 设n为正整数，则2

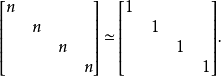
下面引理即著名的Witt消去定理。

引理2设A与B为有理数域Q上两个n×n非奇异对称矩阵，c∈Q且c≠0，若

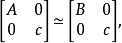则 。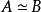

布鲁克-赖瑟-乔拉定理的特例关于Legendre方程存在非平凡整数解的条件，我们有下述经典结果。

定理3 Legendre方程ax²+by²=cz²存在非平凡整数解的充分必要条件是下述三个同余式都有解：

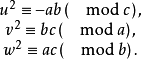
下面给出BRC定理当λ=1时的一个特例。此时定理的形式简洁,应用起来也比较方便。

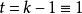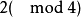定理3 设或且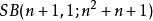存在，则n的无平方因子部分不存在形如4t+3的素因子。

证 显然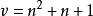为奇数，又n≡1或2(mod 4),因此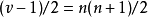也是奇数。从而由BRC定理，从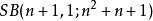的存在性推出不定方程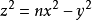有不全为零的整数解，此方程为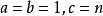时的Legendre方程，由定理3。同余方程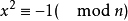有解。从而对n的无平方因子部分的任一素因子p,同余方程有解，因此必有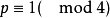。即得结论2。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学