[科普中国]-称重矩阵

称重矩阵(weighing matrix)是阿达马矩阵的推广，若W是元素为0，±1的n阶矩阵，且使WWT=kIn，则称W为n阶称重矩阵，k=n的称重矩阵就是n阶阿达马矩阵，k=n-1的对称称重矩阵就是n阶对称C矩阵，人们猜测：对每个正整数t及每个k=0，1，…，4t，存在4t阶称重矩阵，当k=4t时，这就是阿达马矩阵猜测，若将v阶称重矩阵中的-1换作1，得到的是某个(v，k，λ)-SBIBD的关联矩阵，则称这样的称重矩阵为平衡称重矩阵，这类矩阵的讨论有助于发现新的BIBD设计。1

基本介绍定义 设W为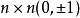-矩阵，若

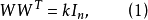则称W为一个重量(weight)k的n阶称重矩阵(weighing matrix)。记作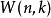。k=n时的称重矩阵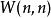便是n阶H-阵。

【例1】设

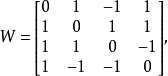则彬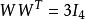，即W为一个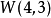。2

相关结论引理1 (Craigen)若4m阶与4n阶H-阵都存在，则存在4mn阶(1，-1)-矩阵S与R满足下述条件：

(i)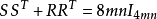， （2）

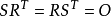(ii)。 （3）

证明设H为4m阶H-阵，K为4n阶H-阵，将它们表为如下形状2：

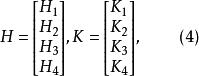其中诸Hi为m×4m矩阵，诸Ki为n×4n矩阵，令

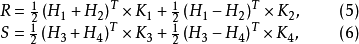则R与S都是(1,-1)-矩阵。由于i≠j时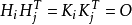。故由引理1得

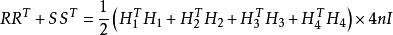
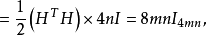
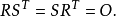即得引理。

引理2 若4m阶与4n阶H-都存在，则存在一对不相交的W(4mn,2mn)。

证明设H为4m阶H-阵，K为4n阶H-阵，R与S分别由式(5)与式(6)给出，令

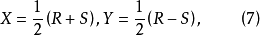于是由式(2)与式(3)得

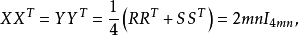即X与Y为一对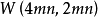。又因R与S都是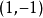-矩阵。故X与Y必不相交。2

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学