[科普中国]-优超关系

优超关系(Superior superrelation)是对策略的概念，设矩阵对策G={S1;S2;A}，其中S1={α1，α2，…，αm}，S2={β1，β2，…，βn}，A=(aij)m×n，如果aij≤akj(j=1，2，…，n)，则称策略αk优超于策略αi。类似地，如果βil≤βij(i=1，2，…，m)，则称策略βl优超于策略βj。1

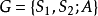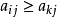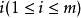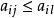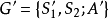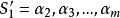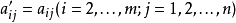基本介绍设是一个矩阵对策，其中。若α1为其余的纯策略之一所优超(若对于一切，均有，则称局中人Ⅰ的纯策略αi优超于αk.同样，对于一切的，均有=，则称局中人Ⅱ的纯策略βj优超于βl)，由G可得到一个新的对策，其中，，则：

1)

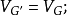
2) G′中局中人Ⅱ的最优策略便是G中局中人Ⅱ的最优策略;

3) 若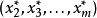是G′中局中人Ⅰ的最优策略，则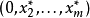是G中局中人Ⅰ的最优策略.

4.对于某些特殊结构的矩阵，可以使其元素尽可能多地变成零.给定两个矩阵对策

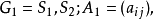
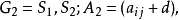其中d是常数，则两个对策的解集合不变，其对策值相差一个d，即(V2和V1分别为G2和G1的对策值)。

如果αi优超于αk，那么当局中人Ⅱ采用任何策略时，Ⅰ采用αk的赢得都不会小于αi的赢得，故可以把αi从Ⅰ的策略集中删去。相应地，删去A的第i行。记新得到的矩阵对策为G1。显然，G1的混合策略解也是G的混合策略解。类似地，如果βl优超于βj，那么，当局中人Ⅰ采用任何策略时，Ⅱ采用βl的付出都不会多于βj的付出，从而把βj从Ⅱ的策略集中删去，相应地删去A的第j列，所得到的矩阵对策的解也必是原矩阵对策的解。利用这个方法可能降低A的阶数，从而减少求解对策的计算量2。

例题解析【例1】 求解矩阵对策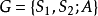，其中

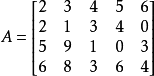解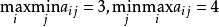，两者不相等，故此矩阵对策没有鞍点。由于根据定义知α1优超于α2，可删去α2及A的第2行，得

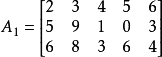对于A1,β1优超于β2，β3优超于β5，可删去β2,β5及A的第2列和第5列，得

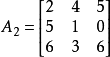对于A2,α4(对应A2的第3行)优超于α3(对应A2的第2行)，又可以删去α3及A2的第2行，得

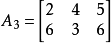对于A3,β1(对应A3的第3列)优超于届，还可以删去β4及A3的第3列，得

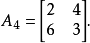最后把问题化成一个2×2矩阵对策，利用公式解得

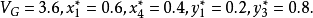
综上可知，局中人Ⅰ的最优策略为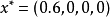，局中人Ⅱ的最优策略为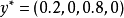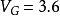，。2

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学