[科普中国]-莫雷拉定理

莫雷拉定理是柯西定理的逆定理。如果函数f(z)在区域D内连续，并且沿着D内任何一条可求长闭曲线γ的积分，那么f(z)在区域D内解析。

简介莫雷拉定理是柯西定理的逆定理。

如果函数f(z)在区域D内连续，并且沿着D内任何一条可求长闭曲线γ的积分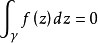 ，那么f(z)在区域D内解析。1

证明在D内任取两点z0和z，因为f(z)在区域B内连续，所以下述积分与路径无关 。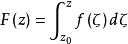

于是可知函数F(z)单值地取决于变量z。同时，易知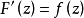 ，所以F(z)是B内的一个解析函数。

由于解析函数的导数仍为解析函数，所以f(z)也是解析函数。2

柯西定理（Cauchy's theorem）

柯西定理是解析函数理论最重要、最基本的定理。

若D是复平面C上的个单连通区域，f(z)在D内是解析的，γ是D内的一条可求长闭曲线，则有

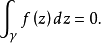
本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学