[科普中国]-G设计

G设计(G-design)是平衡不完全区组设计的一种推广，设G是有k个顶点且无孤立点的简单无向图，λKn是n个顶点的λ重完全无向图，重边看做不同的边，若该完全图能分解成若干个无公共边的子图，每一个都与G同构，则称这样的分解为一个图设计，记为(n，k，λ)G设计1。

基本介绍当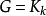 时，一个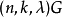 设计就是一个 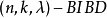。图设计可以看成BIBD设计的区组中引入点之间的某种邻接关系后的推广，这些同构子图称为G区组。当G为有向图时，将 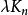改为λ重完全有向图 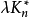，可类似定义 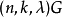设计。当G为无向图且 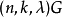设计存在时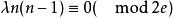， 且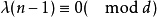 ，式中e是图G的边数而d是G的所有顶点度数的最大公因数。当G为有向图且 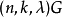设计存在时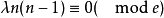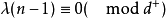， ， 且

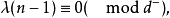
式中的e是图G中弧的条数，而d+与d-分别是所有顶点的出度数的最大公因数及入度数的最大公因数。

黑尔(P.Hell)和罗萨(A.Rosa)于1972年首先引入了图设计这一概念，并研究了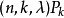 设计的存在性，这里Pk表示k个顶点k-1条边的路，由于图G的变化千姿百态，G设计的存在性研究面广量大，已有结果大多是关于路和圈这些简单而规则的图G的，只有当k较小时才考察所有可能的图G，而完整的结果仅限于k=3，4的情形，图设计的直接构造方法是玻色(R.C.Bose)的对称重差法的变形，而递推构造方法则主要利用多部完全图的分解，与BIBD设计的情形类似，也有可分解性问题以及平衡图设计问题1。

平衡G设计平衡G设计是一类特殊的G设计，若在一个G设计中每个顶点在G区组中出现的次数都相同，则称该图设计是平衡G设计。当G为正则无向图(即顶点的度数均相同的图)或强正则有向图(即每个顶点的出度数和入度数为同一个常数的图)时，G设计总是平衡的，平衡G设计的参数除必须满足一般G设计的必要条件外，还必须满足进一步的条件：当G为无向图时，应有

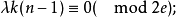当G为有向图时，应有

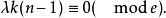当G为k个顶点k-1条边的路或星形图时，平衡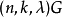设计存在的必要条件也是充分条件，当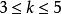且G为无向图时，平衡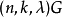设计的存在性也已得到完全解决1。

带洞G设计带洞G设计亦称带洞图设计，用于递推构作G设计的一类辅助设计。设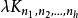是λ重h部无向完全图，顶点集X划分为互不相交的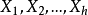，使

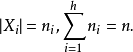设G为k个顶点且无孤立点的无向简单图，若该多部完全图能分解成若干个无公共边的子图，每一个都与G同构，则称这样的分解为一个带洞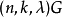设计，称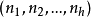为其型，这样的G设计可以看做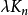的通常G设计中带有一些洞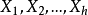，当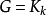时这些洞实际上是可分组设计的组，若每个顶点在G区组中出现的次数相同，则称这种带洞图设计是平衡的，利用带洞图设计可以递推地构造图设计，若存在型为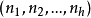的带洞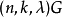设计，且对每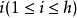存在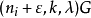设计，其中ε=0或1，则存在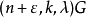设计。特别地，若存在型为(l，l，…，l)的平衡带洞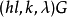设计，且存在平衡的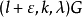设计，其中ε=0或1，则存在平衡的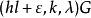设计，对于有向图情形，也可类似定义带洞图设计概念，并且，有相应的递推构造图设计的方法1。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学