[科普中国]-约翰生结合方案

约翰生结合方案(Johnson association scheme)亦称三角形结合方案，是一类度量方案，约翰生结合方案在编码理论中也有重要应用，例如，每一个等重量码都可看做某个约翰生结合方案中的子集1。

基本介绍设，以记某个v元集的k元子集的全体，若当两个k元子集的交为k-i元子集时，规定它们有第i种结合关系，则J(v，k)是有个处理及k个结合类的结合方案，称为约翰生结合方案。当k=2时，约翰生结合方案即为三角形设计中的结合方案，约翰生结合方案在编码理论中也有重要应用，例如，每一个等重量码都可看做某个约翰生结合方案中的子集。

度量方案是一类结合方案，它由距离正则图定义，若Γ为直径d的距离正则图，规定两个顶点的距离为i时它们有第i种结合关系，则在Γ的顶点集合上有一个d个结合类的结合方案，称为度量方案。许多最重要的结合方案都是度量方案。例如，具两个结合类的结合方案一定是度量方案，汉明结合方案与约翰生结合方案也都是度量方案。但是，并非所有的结合方案都是度量方案。1

对三角结合方案的研究1957年起，张里千开始研究试验设计。1959年，张里千对三角结合方案进行了研究，并在较短的时间内解决了这一问题。结合方案是试验设计中部分平衡不完全区组设计(PBIBD)的一种内在数学结构。在三角形结合方案的研究中，张里千用组合数学的方法推导出具有三角参数，和的结合方案唯一地成为三角形方案的一个比较深刻的充要条件，并运用它证明了具有三角参数的结合方案当n≠8时必定是唯一的三角形方案；而当n=8时，除三角形方案外，还构造出全部其他3个方案；从而彻底解决了三角形方案的唯一性问题。在张里千的工作之前，对于n≥9和n=5，6情形已分别被W.S.康纳(Connor，1958年)和S.S.施里克汉德(Shrikhande，1959年)所解决。n=8的情形后来被国外一些图论著作称之为“著名的张图”(well-known Chang graphs)2。

相关介绍三角形设计是一类PBIBD设计，它有两个结合类，设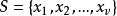，，将S中的v个元以某种次序放在一个n阶方阵的右上角，左下角则放相应元素使该方阵为对称方阵，对角线位置则空着，当S中的两个元xi与xj出现在方阵中的同一行或同一列时，称它们有第一种结合关系；否则，称它们有第二种结合关系。这样便得到S上有两个结合类的结合方案，称为三角形结合方案。集S中相应的PBIBD设计称为三角形设计。三角形结合方案的参数由n确定：当n≠8时，三角形结合方案是在同构意义下由参数惟一确定的；当n=8时，则不惟一。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学