[科普中国]-包容关系

包容关系即集合之间元素的从属关系，也称包含关系，称集合B包容A，记为A⊆B，当且仅当A的元素必为B的元素。包容关系构成组合理论的基本序关系。因为它本身可以构造出典型的组合形态如布尔代数B(2E，⊆)，同时借助于它可以刻画更为复杂的关系1。

基本介绍设f和g均为从集合N到集合M的映射，若只关心N中有多少元素，而不理会是哪些元素映入到它们的像域时，则其像域g(b)可表示为

im(f)={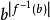|b∈M}，

im(g)={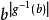|b∈M}.

这样在映射f，g之间建立包容关系：f⊆g当且仅当对M的所有元素b均有|f-1(b)|≤|g-1(b)|。1

定义包容关系也称包含关系，包含是集合与集合之间的从属关系，也叫子集关系。基本含义近同于蕴含、蕴涵、包涵，关系形容词。出自汉·桓宽《盐铁论·地广》：“王者包含并覆，普爱无私，不为近重施，不为远遗恩。”。

设A和B是两个集合，若集合A的元素都是集合B的元素，则称集合B包含集合A，或集合A包含于集合B，记作2

A⊆B或B⊇A.

分类（1）包含于（包含）；

（2）真包含（真包含于）。

性质集合的包含关系有如下性质：设A，B，C为任意三个集合，有

①A⊆A(反身性)；

②若A⊆B，则B⊇A(对称性)；

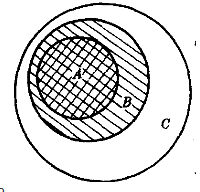
③若A⊆B，B⊆C，则A⊆C(传递性)，图1直观地表示了这一性质2。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学