[科普中国]-拟剩余设计

剩余设计是一种由对称设计导出的平衡不完全区组设计，具体的构作方法如下：设(X，B)是一个(v，k，λ)-SBIBD，取定一个区组B0，对其余的区组B，记B′=B\B0，且B′={B′|B∈B\{B0}}，这样得到的一个区组设计(X\B0，B′)是一个(v-k，v-1，k，k-λ，λ)-BIBD，称为(X，B)的剩余设计。当一个BIBD设计的参数为(v-k，v-1，k，k-λ，λ)时，称为拟剩余设计。若一个拟剩余设计是某个对称设计的剩余设计，则称该拟剩余设计是可嵌入的，利用康纳-霍尔定理可以证明某些BIBD设计不存在1。

基本介绍定义1 若v,k与λ满足条件λ(v-1)=k(k-1)，设D*为一个B(k-λ，λ；v-k)，则称D*为一个拟剩余设计(quasi residual design)。

讨论下面这个问题是有意义的：设D*为一个B(k-λ，λ；v-k)，它是一个拟剩余设计，是否存在一个SB(k，λ；v)使D*作为它的剩余设计?试看下述例子，它实际上给出了当λ=1时从拟剩余设计构作相应的对称设计的一个重要方法。

例1 设V=Z16，D*=(V*，B*)为如下B(4，1；16)：

P₁：{0，1，2，3}，{4，5，6，7}，{8，9，10，11}，{12，13，14，15}；

P₂：{0，4，9，13}，{1，5，10，14}，{2，6，11，15}，{3，7，8，12}；

P₃：{0，5，11，12}，{1，4，8，15}，{2，7，9，14}，{3，6，10，13}；

P₄：{0，6，8，14}，{1，7，11，13}，{2，4，10，12}，{3，5，9，15}；

P5：{0，7，10，15}，{1，6，9，12}，{2，5，8，13}，{3，4，11，14}.

这是一个拟剩余设计，并且是可分解的。它的平行类为Pi，i=1，2，3，4，5，用添加5个无穷远点及一条无穷远直线(即由这些无穷远点组成的新区组)来构作所需的SB(5，1；21)，设1≤i≤5。对Pi中的每一个区组都添加一个无穷远点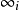 之后当作新区组，然后再添加一个新区组 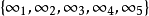，故共得21个区组，由于每一个无穷远点与Z16中每一个元素都恰好相遇一次。任意两个不同的无穷远点也正好相遇一次。因此得到一个SB(5，1，21)。它以D*作为剩余设计2。

利用上面的方法可以证明下述定理。

相关定理定理1 λ=1的任一拟剩余设计都可以作为某个对称设计的剩余设计2。

为证明上述定理，需要下面引理。

引理1 每一个λ=1的拟剩余设计都是可分解的。

证明 设D*为一个拟剩余设计B(k-λ，λ；v-k)，令n=k-1。由k(k-1)=v-1得v=n2+n+1，即v-k=n2，因此D*是一个B(n，1；n2)，它共有b=n(n+1)个区组。并且每一点都恰好包含在n+1个区组中，设A1为D*的一个区组，它的每一点都恰好包含在A1之外的n个区组中，并且A1中任意不同的两点不可能同时包含在A1之外的任意区组中。否则将与λ=1矛盾，由于A1中共有n个点，因此恰有n2个区组与A1相交，并且交点唯一，从而恰有n-1个区组与A1不相交，设为A2，A3，…，An，下面证明A1，A2，…，An组成一个平行类。

对2≤i≤n，Ai中的任一点都必须与A1中的每一点都相遇一次，又因Ai中任意两个不同的点都不可能在Ai之外的任意一个区组中相遇，从而与A1相交的n2个区组中的每一个都与Ai相交，于是A1，A2，...，Ai-1，Ai+1，…，An中的每一个都与Ai不相交，因此A1，A2，…，An组成一个平行类，记为P₁。

设An+1为一个不属于P1的区组，将n-1个与An+1不相交的区组记作An+2，…，A2n。由于An+1与P1中的每一个区组都相交，因此这n-1个区组都不属于P1。同前可证An+1，An+2，…，A2n组成一个平行类，记作P2，P2与P1显然不相交即没有公共区组。一般地。设s≤n，已得到s个互不相交的平行类P1，…，Ps，则在剩下的(n+1-s)·n个区组中必可找到n个互不相交的区组Asn+1，Asn+2，…，A(s+1)n，它们组成一个平行类Ps+1，从而可将D*的全部n(n+1)个区组划分成n+1个平行类，即D是一个可分解设计。

定理1的证明：设D*=(V*，B*)为λ=1的拟剩余设计，则必有正整数n使D*为一个B(n，1；n2)。由引理2，D*的全部区组可划分成n+1个平行类P1，P2，…，Pn+1。设1≤i≤n+1，对Pi中每一个区组都添加一个无穷远点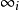 作成新的区组，再将”无穷远直线”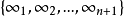也看作一个区组，如此共得n2+n+1个区组,它们组成V=V*∪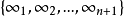上的一个SB(k,1；v),此处k=n+1,v=n2+n+1，显然D*是这个对称设计的一个剩余设计。

当λ=2时，M.Hall与W.S.Connor证明了下面的定理。

定理2 设λ=2，则每一个拟剩余设计都是某个对称设计的剩余设计。

然而当λ≥3时，类似的结论未必成立，即使在λ=3时，也并不是每一个拟剩余设计都可以作为某个对称设计的剩余设计的。

van Lint，Tonchev与Landgev构作出一个B(10，5；28)，这是一个拟剩余设计。SB(15，5；43)不存在，由此给出了第一个这样的例子，即使SB(k，λ；v)不存在，拟剩余设计B(k-λ，λ；v-k)仍然存在。2

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学