协同优化算法的原理是将一复杂的目标函数分解成简单的子目标函数,然后再将这些子目标函数进行协同优化。具体说来,协同优化是在优化每一子目标函数同时综合考虑其它子目标函数的结果,使子目标函数之间的优化结果能够一致。优化结果一致是指使每一变量的值在每一子目标函数的优化结果中能够一致。一般来说,可以证明,如果变量的值一致则为最优解。协同优化算法没有局部最优问题同时具有非常良好的收敛特性。 它很好地解决了许多实际中非线性优化及组合优化难题。
简介协同优化算法的原理是将一复杂的目标函数分解成简单的子目标函数,然后再将这些子目标函数进行协同优化。具体说来,协同优化是在优化每一子目标函数同时综合考虑其它子目标函数的结果,使子目标函数之间的优化结果能够一致。优化结果一致是指使每一变量的值在每一子目标函数的优化结果中能够一致。一般来说,可以证明,如果变量的值一致则为最优解。协同优化算法没有局部最优问题同时具有非常良好的收敛特性。 它很好地解决了许多实际中非线性优化及组合优化难题。
如果目标函数是一n个变量的函数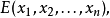 简写成
简写成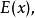 协同优化算法先将它分解成n个简单的子目标函数:
协同优化算法先将它分解成n个简单的子目标函数:
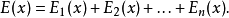
如果单独优化每一子目标函数,则它们的结果很难达到一致。例如,变量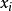 在包含它的子目标函数中的最优解值很难相同。对于
在包含它的子目标函数中的最优解值很难相同。对于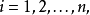 如果我们取
如果我们取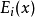 的最优解中
的最优解中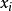 的值作为该变量的值,表示成
的值作为该变量的值,表示成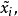
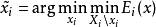 这里,
这里,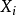 是
是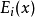 的变量集,
的变量集,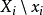 指变量集
指变量集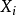 除去元素
除去元素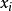 ,
,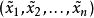 则很难为原目标函数{\displaystyle E(x)}的最优解。为了使子目标函数之间的优化结果能够一致,协同优化算法在优化每一子目标函数
则很难为原目标函数{\displaystyle E(x)}的最优解。为了使子目标函数之间的优化结果能够一致,协同优化算法在优化每一子目标函数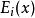 同时考虑其它子目标函数的结果:
同时考虑其它子目标函数的结果:
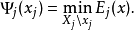
具体做法是利用其它子目标函数的优化结果通过数值加权修正每一个子目标函数如下:
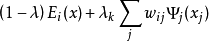 这里,
这里,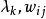 为加权系数,满足
为加权系数,满足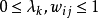 。
。
然后对修正后的子目标函数进行优化,优化结果再叠代放入修正的子目标函数中。协同优化算法的叠代方程如下:
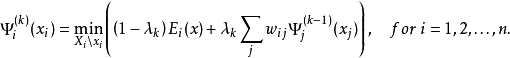
协同优化结果使每一变量的值在每一子目标函数的优化结果中达到一致。如果一致,则子目标函数的优化解既为最优解。1
理论价值现代优化理论中最重要的未解难题是发现通用的全局最优化条件。由于没有全局最优化条件,我们不知道哪里可以找到最优解,也不知道现有解是不是最优解. 因此,我们不知道如何更有效地组织优化过程及何时及时中断搜索。任何全局最优化条件既有理论意义和实用价值。协同优化算法基于一种全新的优化原理解决了这一重要问题。1
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国