[科普中国]-天平问题

天平问题(scales problem)是一种趣味组合计数问题。设有重量分别为a1克，a2克，…，ak克的k个砝码，ai(i=1，2，…，k)均为整数，今要在天平上衡量重为n克的重物，问有多少种不同衡重方法1?“天平问题”在数字游戏和智力竞赛中经常遇到，这类问题种类繁多，构思精巧，解法独特，对发展智力、嘏炼意志有很好的推动作用。“天平问题”主要有：天平挑次品类、天平一边放砝码类和天平两边放砝码类等2。

基本介绍天平问题：设有重量分别为a1克，a2克，…，ak克的k个砝码，ai(i=1，2，…，k)均为整数，今要在天平上衡量重为n克的重物，问有多少种不同衡重方法?

若规定砝码只能加在天平一端，则不同方式总数An的计数生成函数是

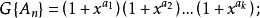
若规定砝码可加在天平两端，则不同方式总数Bn的计数生成函数

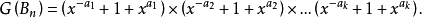
例如a1=1克，a2=3克，a3=4克，a4=6克，则n=6克的不同方式B6有4种，这里砝码放法〈天平左端，天平右端〉是：〈n，6〉，〈n+1，3+4〉，〈n+1+3，4+6〉和〈n+4，1+3+6〉，其中n表示重6克的物体1。

例题解析【例1】2002年1月1日，欧元正式在欧元区12国流通。玮玮的爸爸从法国带回9枚欧元硬币，由于制造的原因，其中有一枚是次品，质量稍微小一点，现在给你一架天平，至少称几次才能把它找出来2？

分析与解 先把这9枚欧元硬币任意平均分成三堆，每堆各3枚，把其中的两堆分剐放在天平的左右两盘中，若天平平衡，说明次品在未放到天平的那一堆中；若天平不平衡，说明次品在质量较小的一个盘子中。接着将混有次品的3枚欧元硬币平均分成三堆，并将其中的两堆分别放在天平的两边再称一次，若天平平衡，说明次品在未放到天平的那一堆中；若天平不平衡，说明次品在质量较小的一个盘子中。因此至少要称2次。

技巧点拨 如果是许多物品里混有一件次品，关键是将所有物品任意地平均分威三堆，取其中两堆放在天平左右盘里看是否平衡，确定有次品的一堆。再重复上面的操作，直到每堆一件，然后将三件中任意两件放在天平左右盘里看是否平衡即可挑出哪一件是次品2。

【例2】18个外表一样的球，有8克和7克两种质量，现在用一台天平来测定每种球各几个。先取两个球，天平的两边各放一个，结果天平不平衡。就拿这两个球作标准，将余下的16个球分成8对，用天平与这对标准球逐一比较，结果3对质量较大，4对质量较小，1对与标准球质量一样。那么这18个球的总质量是多少克？

分析与解 第一次称的两个球，天平不平衡，就知道1个是8克，1个是7克，作为标准的一对球，质量之和是8+7=15（克）。比标准球质量大的一时球，一定是两个8克的球，质量和是16克l比标准球质量小的一对球，一定是两个7克的球，质量和是14克；与标准球质量一样的一对球质量是15克。因此，18个球的质量是：

16×3+14×4+15×2=134(克)

【例3】小明家买回100个鹌鹑蛋，每袋装10个。其中9只袋里装的鹌鹑蛋，每个都是10克。另外一袋装的每个都是9克。这十袋混在一起，只准用天平称一次，你能找出其中一袋装的每个都是9克的鹌鹑蛋吗？

分析与解 把十袋鹌鹑蛋依次编号，从第一袋内取1个，第二袋内取2个，第三袋内取3个……第十袋内取10个，放在一起称，那么共有鹌鹑蛋1+2+3+…+10=55（个）。如果每个鹌鹑蛋都是10克，55个鹌鹑蛋应是550克，从少的质量中就能找到装9克的鹅鹑蛋袋。若少1克，就是第一袋，若少5克，就是第五袋…

技巧点拨 如果是许多袋（箱或盒）中混有一袋（箱或盒）次品且只准称一次，可以将，分别取1个、2个、3个……n个，再求出(1+2+3+…+n)个的质量和即可挑出次品。

【例4】在天平的一端放砝码，另一端放物体，若要称出1～60克之间所有质量为整数的物体的质量，最少应该准备多少个什么样的砝码？

分析与解 要想称出1克物体，必须有1克砝码；再有一个2克砝码，就可以称出2克、3克的物体；第三个砝码应该是3+1=4（克），这三个砝码又能称出1～7克7种质量；第四个砝码应是7+1=8（克），这四个砝码能称出1- 15克的不同质量的物体；第五个砝码是15 +1=16（克），这五个砝码能称出1~31克的不同质量的物体；第六个砝码是31+1= 32（克），这样，就能称出1~63克的不同质量的物体。

所以，要称出1～60克之间各种不同质量的物体，至少应准备1克、2克、4克、8克、16克、32克六种砝码各一个。

【例5】有7克、2克砝码各一个，天平一架，如何只用这些物品三次将140克的盐分成50克、90克各一份？

分析与解 （1）把2克的砝码放在天平左端，分盐于天平两端直至平衡，此时，左端盐的质量为69克，右端盐的质量为71克；(2)取下天平左端的砝码换上7克的砝码，左端的质量为69+7=76（克），右端的质量为71克，从左端取出5克盐后，两端平衡，速时左端尚余64克盐，取下天平两端物品;(3)用刚才称出的5克盐当做“砝码”，与2克、7克砝码合成14克砝码，从64克盐中取出14克，恰好剩下50克盐，则其余盐的质量就是90克。

技巧点拨 砝码称质量是常见的数学问题。不管是挑选次品，还是借助砝码称物体重量，都要进行周全的考虑，可以采用简单的方法发现规律，在“排除”借用”的策略中找到解决问题的思路2。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学