[科普中国]-重量计数子

重量计数子(weight enumerator)是对码的一种度量刻画，它是码的重量分布的生成多项式，设q元[n，k]线性码C中重量为i的码字有Ai个，i=0，1，…，n，则称数列(A0，A1，…，An)为码C的重量分布，而称多项式A(z)=A0+A1z+…+Anzn为码C的重量计数子。当C的极小重量为w时，Aωzw就是A(z)中除常数项外次数最低的项，因此从C的重量计数子可以得到它的极小重量，对于线性码而言，极小重量与极小距离相等，因而对判别码的检错能力与纠错能力十分重要，对此，麦克威廉斯定理提供了一个有效的方法1。

基本介绍线性码的极小距离告诉我们，一个接收字可以含多少个差错但我们仍能正确译码。对码的距离作更详细的了解常常是很有必要的。为此，我们引入所谓码的重量计数子的概念。

定义设C是长为n的线性码，Ai是重量为i的码字的个数，则

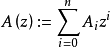称为C的重量计数子，序列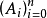称为C的重量分布2。

举例说明作为例子，我们计算长为n的二元Hamming码的重量计数子。考虑这个码的奇偶校验矩阵的i-1个列，共有3种可能2：

(i)这个列之和为0；

(ii)这些列之和是其中某一列；

(iii)这些列之和是余下的列中某一列。

选取i-1个列共有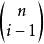 种方法，其中情况(i)出现Ai-1,次，情况(ii)出现(n-(i-2))Ai-2次，情况(iii)出现iAi次，所以

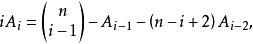
此式在i>n+1时显然成立，两边同乘zi-1，并对i求和，我们发现

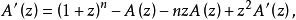因为A(0)=1，这个微分方程有唯一解：

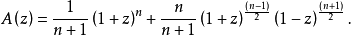
相关定理编码理论中一个最基本的结论是属于F.J.MacWiUiams(1963)的，它给出了一个线性码的重量计数子与其对偶码的重量计数子之间的关系2。

定理 设C是Fq上一个[n，q]码，重量计数子为A(z)，又设B(z)是C⊥的重量计数子，那么

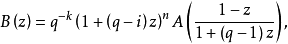
本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学