[科普中国]-麦克威廉斯定理

麦克威廉斯定理(MacWilliams theorem)是关于编码理论中的一个重要结论，它给出了线性码C与它的对偶码C⊥的重量计数子之间的相互联系，这个定理由麦克威廉斯(F.J.MacWilliams)于1962年得到，范·林特(J.H.van Lint)于1971年利用特征标理论给出了该定理的一个简洁证明，若C⊥的重量计数子已知，则该定理给出了关于n+1个未知数A0，A1，…，An的n+1个方程的线性方程组，从而可解方程组求得线性码C的重量计数子。

基本介绍编码理论中一个最基本的结论是属于F.J.MacWiUiams(1963)的，它给出了一个线性码的重量计数子与其对偶码的重量计数子之间的关系。

定理设C是Fq上一个[n，q]码，重量计数子为A(z)，又设B(z)是C⊥的重量计数子，那么1

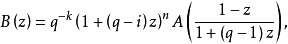
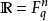麦克威廉斯定理的证明设是(Fq，+)的任意一个非平凡特征标。令，我们定义

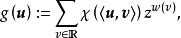则

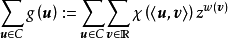
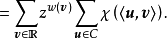若v∈C⊥，则内和是|C|，若v∉C⊥，则内和取到Fq中每个值的次数相同，即内和为0。所以

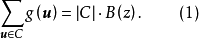
把重量函数推广到Fq上：若v=0，则记w(v)=0，否则记w(v)=1。那么令u=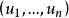，v=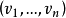后，我们由g(u)的定义得

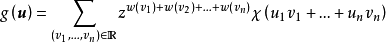
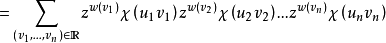
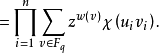在最后的表达式中，内和当ui=0时等于1+(q-1)z，当ui≠0时等于

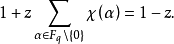因此

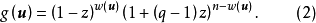
由于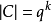，把（2）代入（1）即得定理1。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学