[科普中国]-LD设计

LD设计是一类辅助设计，在解决施泰纳三元系大集问题中由中国的陆家羲引入，这类设计对施泰纳三元系大集问题有重要作用，对别的组合设计的存在性问题也有用，LD(n)的存在性已基本解决，除十几个n值外LD(n)都是存在的1。

基本介绍设X为n元集，L¹与L²分别为X上的正交表OA(n，4)，对每个x∈X，Lx是X\{x}上的正交表OA(n-1，3)（见下文“正交阵列”）。若存在c∈X，使对任一x∈X有(x，x，x，c)∈L¹∩L²，且对任一(u，v，w)∈X³，或存在x∈X使(u，v，w)∈Lx，或存在t∈X及j∈{1，2}使(u，v，w，t)∈Lj，则称{L¹，L²}∪{Lx|x∈X}为LD设计，记为LD(n)。这类设计对施泰纳三元系大集问题有重要作用，对别的组合设计的存在性问题也有用，LD(n)的存在性已基本解决，除十几个n值外LD(n)都是存在的1。

正交阵列正交阵列即正交表，正交阵列是一类组合设计，设A是v元集X上的v×k矩阵，若对任意d(2≤d≤k)列所构成的子矩阵，X上的每一个d元排列作为子矩阵的行各出现λ次，则称A为大小N，约束数k，水平数v，强度d和指数λ的正交阵列，在试验设计中称正交表，记为OA(N，k，v，d)，由定义有N=λvd，强度2的正交阵列记为OA(v，k;λ)，当λ=1时简记为OA(v，k).OA(v，k;λ)的存在性等价于横截设计TDλ[k;v]的存在性，OA(v，k)的存在性则等价于k-2个v阶相互正交拉丁方的存在性1。

相关介绍关于施泰纳三元系大集的研究

陆家羲是获得国家自然科学奖一等奖中唯一的一位普通中学教师。他解决的STEINER三元系大集问题属于组合数学的设计理论领域，是19世纪50年代由Cayley、Sylvester和Kirkman等人提出来的，在组合设计的理论和应用上有重要意义，但是由于问题本身的艰难性，直至本世纪70年代进展甚微。自1972年始，国外一些组合设计学家引进逆推方法，对它有了部分推进，但直到1980年止，结果依然是零碎的，距完全解决相去甚远。陆家羲经过20多年的刻苦钻研，终于在1981-1983年基本上解决了这一难题，对所余的6个未定数值也给出了解决框架。国际组合数学刊物于1981年9月和1983年4月分两期登载了他为解决这个问题所写的6篇文章。这一成果获1987年第三次国家自然科学奖一等奖。2

1981-1983年，陆家羲以16个引理29个定理，严谨地布下整体解决问题的格局，引人各一个递归构造，独创了一系列的辅助设计，运用前人已有的各种结论进行了复杂的计算和归纳，最终证明大集定理：

如果v≡1,3(mod 6)，v>7，和v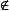{141，283，501，789，1 501，2 305}，那么D(v)=v-2，人们还编成大集定理的算法程序，在计算机上验证了大集定理的结论是完全正确的。

陆家羲的这一成果已载入组合数学史册。3

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学