[科普中国]-着色设计

着色设计(coloured design)是一种特殊类型的图设计，从着色设计可得到别的类型的组合设计，因此，着色设计在一定程度上起着统一不同类型的设计的作用，对k=4及各种可能的着色情况，着色设计的存在性已基本解决。

基本介绍着色设计是一种特殊类型的图设计，设对Kk用c种颜色C1，C2，…，Cc将边着色，着色Ci的边有ni条，着色后的图记为G，以g记所有ni的最大公因数，

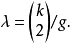将λKn中连结任意两个顶点的λ条边中的ni/g条着色Ci，所得的图记为C°Kn，若C°Kn可以分解为若干子图，使每个子图都与G同构(连同着色)，则称这样的分解是一个着色设计。当c=1时，一个着色(n，k，1)G设计就是一个(n，k，1)-BIBD。当k=4，c=2并使着色C1的边形成长为3的圈，着色C2的边形成一个星形图，则一个着色设计中长为3的圈形成一个STS(n)，而第二种颜色的星形图形成该STS(n)的一个嵌套(参见下文“嵌套”)，当k=4，且{a，b，c，d}上K4的边{a，b}，{c，d}着色C1，{a，c}，{b，d}着色C2，而{a，d}，{b，c}着色C3，利用相应的着色设计的G区组定义顶点集上的一个幂等拟群，使

a°b=c，b°a=d，c°d=a，d°c=b，

则该幂等拟群必满足拟群恒等式xy°yx=x(参见下文“拟群”)，从着色设计还可得到别的类型的组合设计，因此，着色设计在一定程度上起着统一不同类型的设计的作用，对k=4及各种可能的着色情况，着色设计的存在性已基本解决1。

相关概念嵌套嵌套是由已知图设计构造新的图设计的一种方法，以Ck表k个顶点k条边的无向圈，以Sk+1表k+1个顶点k条边的星形图，若对一个(n，k，1)Ck设计存在一个映射f，将每个圈B映为不在B中的某个顶点f(B)，并且使所有的星形图Kk+1-B(Kk+1)的顶点集V(B)∪{f(B)}，它形成一个(n，k+1，1)Sk+1设计，则称映射f是一个嵌套，当(n，k，1)Ck设计有嵌套映射时，称该设计是可嵌套的。若用Wk+1表示k+1个顶点2k条边的轮形无向图，则从一个可嵌套的(n，k，1)Ck设计可得到一个(n，k+1，2)Wk+1设计，一个(n，k，1)Ck设计可嵌套的必要条件是n≡1(mod 2k)，史汀生(D.R.Stinson)于1985年证明：当k=3时，这一必要条件也是充分条件，史汀生等人还证明：对每个整数k≥3，除了至多13个可能例外的n值，这个必要条件也是充分条件1。

拟群拟群是一种代数系统，设集Q上有一个二元运算称为乘法，记为“°”，若对Q中任意元a，b，方程a°x=b及x°a=b在Q中都恰有一个解x，则称(Q，°)为一个拟群，当Q为有限集时，Q中元素个数称为拟群的阶，在n阶拟群(Q，°)的乘法表中，第a行第b列的元素为a°b，若记L=(mab)，mab=a°b，则由乘法表所得的阵列L是一个n阶拉丁方，反之，由一个n阶拉丁方作为乘法表所得的二元运算形成集Q上的一个拟群，若对拟群(Q，°)中的每个元x恒有x°x=x，则称该拟群是幂等的，若集Q上有n-2个n阶幂等拟群，使对Q中任意两个相异元a，b，集Q上n-2个值a°b取遍Q\{a，b}，则称这n-2个拟群构成一个幂等拟群大集.已知当n≥3且n≠6时，n阶幂等拟群大集总存在，而6阶幂等拟群大集则不可能存在1。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学