[科普中国]-极大距离可分码

极大距离可分码(maximum distance separable code)亦称MDS码，指达到辛格尔顿界的码。若M=qn+1-d，则称q元(n，M，d)码为极大距离可分码，当n-d+1=2时，q元(n，q2，d)MDS码的存在性等价于n-2个q阶相互正交拉丁方的存在性，当C为[n，k，d]线性码时，C为MDS码的充分必要条件为d=n-k+1，MDS线性码有许多有趣的性质，例如，MDS线性码的对偶码也是MDS码，一个[n，k，d]线性码是MDS码的充分必要条件为生成矩阵中任意k列均线性无关，此外，若在射影几何PG(k-1，q)中存在n个点的集合S使其中没有k个点位于同一个超平面内，则存在一个[n，k，d]MDS码1。

基本介绍定理1辛格尔(Singleton)顿界 设是一个参数为[n,k]的线性码，则C的极小距离d≤n-k+1。

以上表明一个线性码的极小距离不会“太大”，无论怎样努力，都不能够构造出一个参数为[n,k]的线性码，使得它的极小距离大于n-k+1，由此可见，最好的期望就是构造使得极小距离等于n-k+1的线性码，于是引出下面的定义2。

一个参数为[n,k]的线性码C，若满足dmin(C)=n-k+1，则称该码为极大距离可分码，简称为MDS码。

事实证明，MDS码是存在的，下面广义Reed-Solomon码就是MDS码。

相关介绍证明定理1之前先介绍一个定理，下面的定理揭示了线性码的校验矩阵与其极小重量亦即极小距离之间的关系2。

定理2设 是一个参数为[n,k]的线性码，令u∈C，WH(u)=m，C的校验矩阵为H,则H中有m列存在一个线性相关关系。反之，对于H的m列中任何一个线性相关关系，都对应一个C中重量不大于m的码字。

证明：因为u∈C，H是C的校验矩阵，所以HuT=0，又WH(u)=m，去掉u的零分量，这正是H的m列的一个线性相关关系。因此，H中有m列存在一个线性相关关系。反之，如果H的m列有一个线性相关关系，则存在m个不全为零的系数，使得这m列的线性组合等于零，现在定义一个一维行向量u：与这m个列对应的分量就取对应的这m个系数，其余分量取零。显然，WH(u)≤m,HuT=0，所以，u是一个C中重量不大于m的码字。

推论1设 是一个线性码，C的校验矩阵为H，则C的极小重量亦即极小距离为d当且仅当d=max{m|H的任意m-1列都线性无关}。

证明:由定理2可得。

定理1的证明：设参数为[n,k]的线性码C的校验矩阵为H,则H是一个秩为n-k的(n-k)×n矩阵，因此，H中的任意n-k+1列都线性相关。由定理2可知，

d≤n-k+1。

极大距离可分码举例Reed-Solomon码 一个Reed-Solomon码(RS码)是Fq上长为n=q-1的本原BCH码，这种码的生成元具有形式g(x)=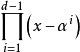，其中α是Fq的一个本原元。

下述定理3的系理实际上就是说Reed-Solomon码是极大距离可分码。

定理3设计距离d的码长q-1的q元Reed-Solomon码的极小距离等于d.。

系理 设计距离d的码长n=q-1的q元Reed-Solomon码的码长n，信息位的个数k和极小距离d三者之间适合关系式：

d=n-k+1.

注意，一般说来，我们有：3

定理4 (n，k)线性码的极小距离d≤n-k+1。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学