[科普中国]-度量方案

度量方案(metric scheme)是一类结合方案，它由距离正则图定义，若Γ为直径d的距离正则图，规定两个顶点的距离为i时它们有第i种结合关系，则在Γ的顶点集合上有一个d个结合类的结合方案，称为度量方案1。

基本介绍度量方案由距离正则图定义，若Γ为直径d的距离正则图，规定两个顶点的距离为i时它们有第i种结合关系，则在Γ的顶点集合上有一个d个结合类的结合方案，称为度量方案。许多最重要的结合方案都是度量方案。例如，具两个结合类的结合方案一定是度量方案。汉明结合方案与约翰生结合方案也都是度量方案。但是，并非所有的结合方案都是度量方案。

距离正则图(distance-regular graph)是一类与结合方案有关的图，设Γ是一个连通图，有v个顶点，无环边及重边，Γ中两顶点间的距离是连结这两点的最短路所含的边数，Γ中任意两个顶点之间距离的最大值称为Γ的直径，若对Γ中距离为k的任意两个顶点x，y，与x的距离为i且与y的距离为j的顶点z的个数是一个常数Cijk，与x，y的选择无关，则称Γ为距离正则图，直径为2的距离正则图称为强正则图1。

举例约翰生结合方案约翰生结合方案(Johnson association scheme)亦称三角形结合方案，是一类度量方案，设k≤v/2，以J(v，k)记某个v元集的k元子集的全体，若当两个k元子集的交为k-i元子集时，规定它们有第i种结合关系，则J(v，k)是有

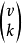个处理及k个结合类的结合方案，称为约翰生结合方案。当k=2时，约翰生结合方案即为三角形设计中的结合方案。约翰生结合方案在编码理论中也有重要应用，例如，每一个等重量码都可看做某个约翰生结合方案中的子集。

汉明结合方案汉明结合方案(Hamming association scheme)亦称超立方体结合方案，是一类度量方案，结合方案的一种，设H(n，q)是一个q元集合上的有n个分量的有序组的全体，若两个有序组恰好在i个位置上的分量不同，则称它们的汉明距离为i，将H(m，q)取作处理的集合，两个有序组的汉明距离为i时称它们有第i种结合关系，便得到具q个处理及n个结合类的结合方案，称为汉明结合方案。

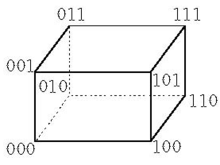
例如，当n=3且q=2时，汉明方案可用下面的立方体表示，立方体的8个顶点表示方案的8个处理，从顶点x到顶点y若至少需经过i条边，则表示处理x与处理y有第i种结合关系。汉明结合方案中的一个子集称为一个码，因此汉明结合方案在编码理论中有重要的应用一类结合方案。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学