[科普中国]-勒贝格有界收敛定理

在数学分析和测度论中，勒贝格有界收敛定理又叫勒贝格控制收敛定理，它提供了积分运算和极限运算可以交换运算顺序的一个充分条件。在分析逐点收敛的函数数列的勒贝格积分时，积分号和逐点收敛的极限号并不总是可以交换的。

控制收敛定理说明了，如果逐点收敛的函数列的每一项都能被同一个勒贝格可积的函数“控制”（即对变量的任何取值，函数的绝对值都小于另一个函数），那么函数列的极限函数的勒贝格积分等于函数列中每个函数的勒贝格积分的极限。勒贝格控制收敛定理显示出勒贝格积分相比于黎曼积分的优越性，在数学分析和实变函数论中有很大的应用。

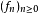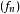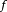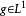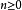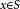定理叙述设为一个测度空间， 是一个实值的可测函数列。1如果逐点收敛于一个函数，并存在一个勒贝格可积的函数，使得对每个，任意，都有：

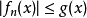
则：

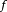也是勒贝格可积的，；

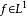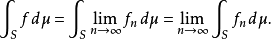其中的函数一般取为正值函数。函数列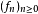的逐点收敛和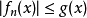的性质可以减弱为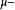几乎处处成立。

证明勒贝格控制收敛定理是更广泛的法图-勒贝格定理（Fatou–Lebesgue theorem）的特例。以下是一个应用法图引理的证明。

由于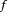 是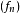逐点收敛的极限，因此对其仍然有

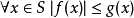（于是）。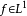

同理，对任意的n有：

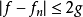
以及

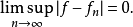
根据法图引理，可以得到：

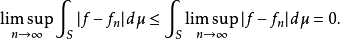
因此，由勒贝格积分的线性性和单调性，就有：

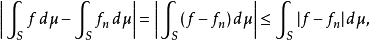
而后者趋于0，于是定理得证。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学