[科普中国]-下极限函数

下极限函数是为判断函数下半连续性而引进的一个概念。设f(x)是定义在点集E上的扩充实值函数，若在闭包E内的点x的δ邻域与E的交内，函数f所取的值的下确界为m(x)，则m(x,δ)在δ趋于0时的极限称为f(x)沿E的下极限函数。

简介下极限函数是为判断函数下半连续性而引进的一个概念。

设f(x)是定义在点集E上的扩充实值函数，若在闭包E内的点x的δ邻域与E的交内，函数f所取的值的下确界为m(x)，则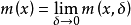 称为f(x)沿E的下极限函数。1

性质当x0∈E，m(x0)=f(x0)时，即-f(x)在x0上半部分连续时，称f在x0处下半连续。当x0∈E，M(x0)=f(x0)时，称f在x0处上半连续。这两种情形统称为f在x0处半连续。2

下确界“下确界”是数学分析中的基本概念，它是在“下界”的基础上定义的。

任给一数集E，我们称E的最大下界为E的下确界，记为infE. 显然，E中每个元素均大于或等于infE。

上极限函数上极限函数是为判断函数上半连续性而引进的一个概念。

设f(x)是定义在点集E上的扩充实值函数，若在闭包E内的点x的δ领域与E的交内，函数f所取的值的上确界为M(x)，则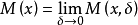 称为f(x)沿E的上极限函数。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学