[科普中国]-本性有界函数类

本性有界函数类又称L空间，是在一个零集之外有界的函数的全体。这样函数的全体称为E上的本性有界函数类，记为L∞(E)或L∞。

简介本性有界函数若E为Rn中的可测集，f(x)是E上的可测函数，且存在零集E0⊂E，使得f(x)在E\E0上有界，则称f(x)为E上的本性有界函数。

本性有界函数类本性有界函数类又称L空间，是在一个零集之外有界的函数的全体。

这样函数的全体称为E上的本性有界函数类，记为L∞(E)或L∞。

范数对f(x)∈L∞(E)，定义f(x)的L∞范数为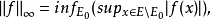其中E0为E的零子集，下确界是对所有可能的这种子集E0而取的：

1、若{fn(x)}⊂L∞(E)，则{fn(x)}在L∞(E)中收敛于f(x)等价于{fn(x)}在E上除一个零集之外一致收敛于f(x)。

2、L∞(E)是巴拿赫空间。

3、L∞(E)不自反。

4、设m(E)