[科普中国]-金属电子论

金属电子论（electron theory of metals）是指研究金属中电子态和电子特性的理论。金属独具良好的导电和导热特性来源于其中有电子气体。20世纪初，P.德鲁德和H.洛伦兹提出经典的自由电子气体模型，认为金属中所有价电子都脱离各自的原子，在整块金属中自由运动，称为金属自由电子气体。这个理论成功地给出欧姆定律的微观图像，并导出金属电导和热导本领之间的关系，即维德曼－夫兰兹定律。但它不能解释为何在常温时 实验上看不出电子气体对比热的贡献1。金属电子论从电子的运动状态阐述金属的结构与特性。

理论1928年A.索末菲用量子力学来表述自由电子的状态，即波矢为k的平面波，而k与电子动量成正比：

p=ħk

ħ为普朗克常数除以2π。按照泡利不相容原理，动量p的状态最多只容纳自旋相反的两个电子。自由电子能量：

E=(px2+py2+pz2)/2m

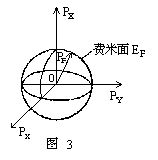所以，在以px、py、pz为轴的空间中等能量的曲面是一个球面。在绝对零度，所有电子填满能量小于和等于EF的全部状态。能量EF的等能面称为费米面。当金属温度达到T时，热运动的能量为kT，k为玻耳兹曼常数。只有能量在EF－kT至EF范围的电子，吸收热能后可跑到能量高于EF的空状态。这部分电子数与电子总数之比约为kT/EF。在常温下kT约等于2.5×10－2电子伏，而EF对大多数金属为几个电子伏，比值在千分之几到百分之一范围。因此，常温下测不到电子气体对比热的贡献。同年，F.布洛赫考虑到金属晶体中原子实有规则地排列形成晶格，电子在晶格周期场中运动，其量子态不再是平面波，而是受晶格周期场调制的布洛赫波。布洛赫波是振幅呈周期变化的平面波，它是周期场中电子的本征态，不随时间变化。在布洛赫波的状态中，电子有确定的能量和确定的波矢k，行为像自由电子。原子价电子的本来能级为Ei，在形成晶体时由于相邻原子之间电子态的交叠、存在相互作用能J，每个原子有Z个最近邻原子，该能级被展宽成能量宽度为B=2ZJ的一个能带。布洛赫的工作为固体能带理论奠定了基础。1

固体能带理论的发展是以哈特里－福克近似下得到的自洽场中单电子方程的解为基础的。自洽场具有晶格的周期性和对称性，计入自旋取向相同的电子之间的交换能。根据电子气体模型，不同金属只是它们的电子密度不同，费米能量或费米球面的半径不同。而在能带理论中，不同的金属的能带结构不一样，有各自的费米面的几何曲面，导致它们对外场响应表现出各有个性。20世纪60年代，W.科恩和P.霍亨伯格提出电子密度泛函理论，认为系统的基态性质取决于系统中的电子密度的分布。孔恩和沈吕九依此理论建立了单电子在有效自洽场中决定其状态的方程。计算机技术的发展和计算方法的改进，能够更精确地计算具体晶体的能带结构，特别是金属电子费米面的具体形状，而种种探测技术使金属的电子结构和费米面能够实验测定。建立了适合过渡金属和稀土金属的电子结构的理论，对于认识这些金属的结合能和磁性至关重要。不但金属的许多物性测量可检证材料能带结构的特征，而且由角分辨的光电子谱的测量可直接得到金属中电子能量与波矢的关系，即电子能谱本身的结构。能带计算为开发新材料而进入工程领域提供了物理基础1。

能带理论虽很成功，但没有充分考虑电子间相互作用引发的集体运动和关联效应。早在20世纪30年代E.维格纳提出，对于密度很低的电子气，系统的动能很小，电子间库仑排斥作用占主导地位。他证明电子有规则地排成晶格比电子均匀分布的状态具有更低的能量，这就是维格纳（电子）晶格。几十年来，科学家一直在寻找维格纳晶格的实例，但未有确证1。
20世纪50年代，D.玻姆和D.派尼斯提出描述电子集体运动的方法，指出金属中由于电子间的相互作用可以出现一些电子集体的振荡模式，称为等离激元。然而，与金属导电导热等输运过程有关的却是比等离激元能量小得多的低能量激发（见固体中的元激发）。认为金属可看成为由带正电的原子实与价电子转化的电子气组成的等离子体。电子间由于库仑排斥作用的驱动，一部分电子被推离原来位置，那里的正电荷增多，从而吸引其他电子，如此反复形成振荡。这种振荡的最小能量单元称作等离体子，各种金属的等离体子大约为几个到几十个电子伏。常温T下的热运动能量为kT，它只有2.5×10－2电子伏。这么小的热运动能量不能激发等离子振荡的自由度，但可激发费米面附近的电子参与电导和热导过程。

L.朗道把金属中有相互作用的多电子系统看成为费米液体。费米液体理论指出，有相互作用的多电子系统的低激发谱与没有相互作用的单电子系统定性地相似，可以用和单电子一一对应的准电子运动来描述，从而解释了单电子能带论在许多情况下可以成功应用的原因。费米液体的低能量激发即低能元激发，具有粒子的性状，与无相互作用的电子气体中单电子的性状相似，故称为准电子，从而阐明了能带理论中的电子能谱的意义。

量子场论在粒子物理领域卓有成效，该法亦适用于自由度无限多的系统。许多学者就利用量子场论方法分析多体相互作用的格林函数方法，研究金属中的多电子问题，特别是阐明和解决了金属超导电性等复杂的物理问题。

当需要考虑各种金属的特殊性来处理多电子问题时，通常采用单电子能带论的计算结果作为起点。因此单电子能带论与多电子理论方法在解决复杂的现代课题中常是相辅相成的。

含有多种不同原子的合金中的电子运动，既具有金属中电子运动的普遍规律性，又有其新的特殊规律性。反映这种特殊规律性的合金电子理论，是金属电子论中近年来发展很快的一个重要方面2。

概念金属电子论是研究金属中电子运动状态的理论。金属特有的良好导电、导热性质是由其中的电子决定的。20世纪初P.德鲁德和H.洛伦兹提出了经典的自由电子模型，这个理论成功地解释了欧姆定律和反映电导与热导之间联系的维德曼－夫兰兹定律。1928年A.索末菲用量子力学和费米-狄拉克统计的原理来描述金属电子的运动，解决了这个问题。同年F.布洛赫进一步考虑原子规则排列的晶体中的周期势场对单个电子（简称单电子）运动的影响，奠定了单电子能带论的基础。他指出，在严格的周期势场中，单个电子处于一个本征态，并且不随时间变化；而在实际晶体中，由于原子热运动或点阵缺陷以及杂质原子，引起偏离严格周期势场的扰动，使单电子的运动状态改变，导致电子散射。这个理论反映出各种晶体的特殊性，并考虑了电子与点阵振动的相互作用，对于描述金属中的电传导、热传导等输运过程，取得了很大的成功2。

电子论阐述：

①单个电子在金属中受到的作用力，以及在其作用下电子的运动状态；

②金属中数量极大，本质上相同的电子在不同的能量状态中的分布；

③在前二者的基础上对电子进行统计研究，获得有关的宏观性质。 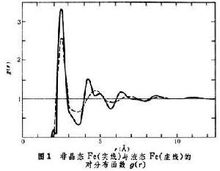金属中的传导电子，既受到所有离子实的作用，也受其他众多的传导电子的作用。
早期的经典电子论，把金属中的传导电子作为在金属内部自由运动的经典粒子。除碰撞外不受点阵离子实的作用。它们相当于容器中自由运动的理想气体的分子（因而称为自由电子气），电子的能量是可以连续变化的，自由电子气服从玻耳兹曼分布律3。
量子力学建立之后，用以处理自由电子运动，并采用量子统计，使自由电子论得到了发展。后来又用周期场来反映离子实点阵的作用，得到了能带理论。3
在具有周期起伏势场的离子实点阵中，在相邻两阵点间的中点附近，场强接近于零；但在离子实中心附近，电子受到很强的吸引力，处理这个问题可以有不同的近似方法。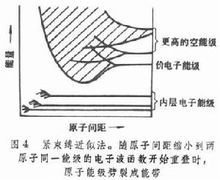

具体解释近自由电子理论以自由电子状态作为起点，考虑一个微小起伏的周期势场的影响，用微扰法解薛定谔方程。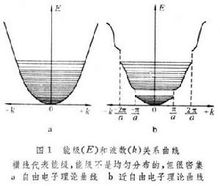图 1b是一维情况下的主要结果（图 1是自由电子论中自由能级和波数的关系曲线）。对于大多数能级，电子和自由电子相似，E－k曲线仍为抛物线，E为电子能量，k为电子波数3。

曲线在某处发生间断，出现能隙，E－k 曲线偏离原来的抛物线。准连续的能级分成一些能带，电子不能具有能隙内能级的能量（即禁带），能隙宽度决定于周期势场相应的傅里叶分量，因而与该方向上的点阵周期和势函数的形式有关。出现间断的条件相当于电子波在相应晶面反射的布喇格条件nλ=2dsinθ（d为晶面间距，θ为入射波与晶面的夹角）3。

三维晶体中的能隙用布里渊区描述。布里渊区是按照金属点阵周期性在/K/空间中划出的区域，即由原点和倒易阵点联线的垂直平分面划出的。例如对一个简单立方点阵，以原点为中心，由六个平面包围的立方体即第一布里渊区。由更远的阵点可构成第二、第三······等区。图2 画出第一、二两区的kx－ky截面。每个方向上的E－k关系具有图1b的特征，可以将三维空间等能面的截面同时表示于图2中。 远离布里渊区边界的等能面保持自由电子的球面，接近区界发生偏离。 随|/K/|的增加，能量增加逐渐变缓，等能面向外突出，但不能穿过区界。和自由电子论对照，能带理论的一个能区的ρ(E)（态密度即在电子能量E与E+ΔE之间具有的能级数）与E的关系曲线如图3所示。在初始阶段接近抛物面，当等能面与布里渊边界接触时对应最大的态密度，此后继续提高能量只有布里渊区角上的状态可以填充，因此愈来愈少3。

电子按照费米-狄拉克分布律每个能级只能有两个电子，从低能态到高能态填充布里渊区。能区仅部分填充的，例如一价金属共有N个电子，只填充一半，则形成导体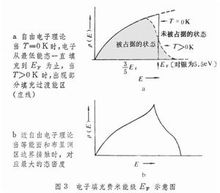，因为能区中尚有大量空态，电子可以从外加电场获得微小附加动能向上跃迁而导电。若电子数正好填满能区，例如2N、4N······则可能有两种情况：由于三维空间中，各方向的能隙大小可能不同，如两个区所对应的上、下能带之间有禁带相隔，即第一区各方向的最高能级均低于第二区的最低能级，则成为绝缘体；如两个能带相互重叠，即第一区有些方向的最高能级比第二区某些方向的最低能级高， 此时电子在第一区未填满时就开始填充第二区，因而也可成为导体，如二价的金属；若低能带虽已填满，但禁带窄，满带顶部的电子可吸收能量而跃迁到上面的空带，变成传导电子，同时满带缺失电子的空态也可在外场作用下转移，产生空穴导电性。本征半导体属于这个类型。也可能由于杂质产生传导电子和空穴，如掺杂半导体。3

紧束缚近似法以电子被束缚在各孤立原子的状态为起点，考虑结合成金属后近邻原子的相互作用。设想两原子相互接近，当原子间距缩小到两原子同一能级的电子波函数开始重叠时，该能级便分裂为二，裂距随原子间距的缩小而变大 。类似地，N个原子结合成固体时，一个原子能级分裂成N个次能级，对应着N个单原子波函数不同线性叠加而组成波函数，这N个次能级形成一个准连续的能带，可容纳 2N个电子。随着原子间距的缩小，原子能级劈裂成能带的情况。距离愈近，能带愈展宽。但不同能级受影响程度不同，最先分裂的是价电子能级，内层电子能级只在原子非常接近时才分裂。紧束缚法直接将孤立原子能级和能带联系起来，因此和近自由电子法可以互为补充。但由于起点不同，其结果的适用性不同，近自由电子论较适于接近自由的传导电子，例如碱金属价电子，紧束缚法则对于比较局限于所属原子附近的电子较为适用3。

其他方法（例如过渡族金属的d电子），均系采用单电子近似，没有考虑电子之间的交互作用，更精确的理论要求计入电子的相互关联。除此以外，还有元胞法、正交平面波法及赝势法等方法，其目的都是为了使计算更精确、更符合实际。3

其他方法上面方法(例如过渡族金属的d电子),均系采用单电子近似，没有考虑电子之间的交互作用，更精确的理论要求计入电子的相互关联。除此以外，还有元胞法，正交平面波法及赝势法等方法，其目的都是为了使计算更精确、更符合实际。

本词条内容贡献者为:

石季英 - 副教授 - 天津大学