[科普中国]-事件代数

事件代数(event algebra)是一种特殊的布尔代数，设P(Ω)是适合某种条件的所有事件的全体，Ω与∅分别是必然事件与不可能事件，∪，∩，-分别是事件的和、积、逆运算，则布尔代数〈P(Ω)，∪，∩，-，Ω，∅〉称为事件代数1。

基本介绍事件代数是用于合成事件(适当定义的理想试验的结果)的模型。如果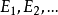表示这种事件，那么：

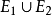表示事件(命题)E1或E2(或者二者，可兼的或)。

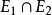表示事件(命题)E1且E2。

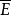表示事件(命题)非E。

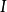表示必然事件(所有可能结果的并)。

O表示不可能事件2。

事件代数亦称事件场、事件域。理论概率论中的概念，是关于一切有限次的运算封闭的非空事件组。称事件组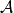为一事件域，如果满足条件：1. 必然事件Ω∈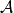; 2.若A∈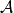，则其对立事件Ā∈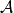;3.若对于任意n≥2， 事件A1， …，An∈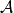，则Ai∈。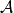

任何事件域都含必然事件和不可能事件；若n个事件属于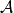，则它们经有限次并、交、相减，所得结果仍然是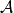中的事件。

相关说明事件代数是由二元布尔代数的另一解释导出一种可应用于概率论的数学模型，概率论研究的是事件发生的可能性；所谓事件，指的是试验或观测的结果。比如投掷一枚骰子是一种试验，而掷出特定的点数，如4，就是一个事件；因骰子有六个面，所以在这种情况下共有六个可能事件3。

在一次给定的试验中，一个事件可能发生也可能不发生，若令事件的发生、不发生分别对应于二元布尔代数中的1，0，就得到一个一一对应。

对于事件定义两种运算——并(或逻辑加法)与交(或逻辑乘法)，这两种运算等价于圻取与合取。

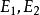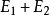事件的并记作。于是，若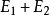=1，则或是E1发生，或是E2发生，或是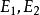两者都发生。类似地，若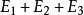=1，则事件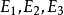中至少有一个发生，并运算相当于二元布尔代数中的加法。

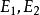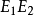事件的交记作，于是，若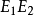=1，则E1与E2两者同时发生，交运算相当于二元布尔代数中的乘法。

事件E的补(互补事件或对立事件)记作E'，若E=1，则E'=0；若E=0，则E'=1。

事件的交与并的运算表与二元布尔代数的运算表完全相同，因此，在交、并运算下事件构成的代数与逻辑乘法、加法运算下的二元布尔代数同构，从而布尔代数的公理、定理对于事件都成立，文氏图也可用来说明事件的组合，以上这些结论在概率论中都有应用。

还要指出包含关系的一个重要结果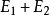：=E1或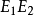=E2，都表示E2包含于E1之中，因此，当且仅当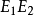=0时，我们说E1与E2是互斥的3。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学