[科普中国]-可构造性公理

可构造性公理(axiom of constructibility)是集合论的一条重要公理，该公理断言：所有集合都是可构造的。哥德尔(K.Gödel)为了证明连续统假设与ZFC是相容的，在1939年第一次构造出集合论的一个非平凡的模型，称为可构造模型。在该模型中连续统假设成立，在构造模型时，哥德尔从无穷公理出发，用超穷递归方法逐步定义出一些集合，这些集合称为可构造集，最后以所有可构造集所组成的集族作为该模型的集合1。

基本介绍可构造性公理(the axiom of constructibility)是集合论的重要假设之一，即命题“每个集合都是可构造集”，记为V=L(参见下文“可构造性”)，可构造性公理虽被称为公理，但人们并不把它视为像ZF系统的基本公理一样理所当然地为“真”，也不把它作为一个新的集合论基本假设加到ZF或ZFC公理系统上，之所以称之为公理，是因为它是一个非常强的集合论命题，在可构造公理下，许多重要的不能由ZF系统或ZFC系统决定的集合论假设(如广义连续统假论、选择公理、某些组合原则等)就可以被确定下来。

美籍奥地利数学家哥德尔(K.Gödel)和美国数学家科恩(P.J.Cohen)分别证明了可构造性公理相容且独立于ZFC公理系统，可以用构造性公理扩充ZFC系统，以便获得更多相容于ZFC系统的集合论命题，这方面的研究构成了可构造性理论的主要内容，然而并没有任何迹象表明可以将可构造性公理作为集合论基本假设加到ZFC公理系统中，相反地，随着大基数理论的研究，人们发现某些大基数的存在性与可构造性公理相悖，如假设可测基数存在，则可以证明存在不可构造的集合，而某些大基数的存在性似乎比假设可构造性公理更具直观基础，尽管如此，可构造性理论作为一种集合论相容性与独立性证明的强有力的工具，仍然被广泛研究与应用2。

可构造性可构造性(constructibility)是一种可构造集理论，是研究集合的可构造性以及可构造集合的各种特殊性质的理论，也是证明集合论命题相对相容性的一种重要方法，集合论的可构造性由美籍奥地利数学家哥德尔(K.Gödel)于1938年在证明选择公理相对于ZF系统，及连续统假设相对于ZFC系统的相容性时提出.在ZFC系统中，似乎所有集合都可以通过累积分层的方法从空集开始，通过反复运用幂集运算构造出来，即令R(0)=0，R(α+1)=P(R(α)).当α为极限序数时，

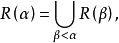则

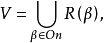这里On为所有序数构成的类。然而，这种构造只说明了V的构造过程，并不是V中的每个元素都可以用这种方法构造出来，也就是说，ZFC系统只提供了构造出一个集合框架的手段，而未曾提供构造框架中每个元素的方法，其原因在于幂集运算似乎将集合扩充得过大，使得人们只能说明对任何集合x而言，x的所有子集可以构成一个新的集合P(x)，但P(x)究竟包含了哪些元素，却无法在ZFC系统中具体地描述出来。例如，不能一一定义出P(ω)中的所有元素，否则P(ω)的基数就可以轻松地确定下来，从而也就可以解决连续统假设问题，为了限制幂集运算，哥德尔利用“可定义幂集”取代幂集，所谓一个集合x的可定义幂集Def(x)，指包含能用集合论语言定义出的所有x的子集(参见“可构造集全域”)，因此，一旦x已知，则Def(x)中的每个元素也可描述，令L(0)=0，L(α+1)=Def(L(α))，当α为极限序数时，

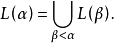称{L(α)：α∈On}为集合的可构造分层，再令

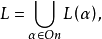称L为可构造集全域，L中的元素称为可构造集，可构造集一定为集合，但随之而来的一个问题是：是否每个集合都是可构造集，即是否有L=V，通常把假设“V=L”称为可构造性公理，哥德尔1938年证明，可构造性公理与ZFC系统相容，亦即在ZFC系统中无法证明V≠L，后来，美国数学家科恩(P.J.Cohen)于1963年利用力迫法证明了V≠L与ZFC系统也相容，从而得出可构造性公理独立于ZFC公理系统，尽管在ZFC系统中无法确定每个集合是否都是可构造集，但人们可以通过可构造集的特别的构造方式获得有关可构造集的若干特殊性质，由可构造性公理相对于ZFC系统的协调性可知，这些性质也协调于ZFC公理系统，以这种方式可以获得大量集合论相容性结果，这种相对相容性证明方法称为可构造性方法，选择公理相对于ZF系统的协调性以及连续统假设(包括广义连续统假设)相对于ZFC系统的协调性正是利用这种方法获得的，另外许多重要的组合原则、大基数性质及一些拓扑学性质相对于ZF系统或ZFC系统的协调性也可以利用这种方法得到证明，法国数学家、工程师莱维(A.Lévy)与休恩菲尔德(J.R.Shoenfield)等人于20世纪50年代末期，在哥德尔可构造性方法的基础上，发展了一种更为灵活的可构造性理论，称为相对可构造性，目前可构造性理论已经成为现代集合论的一个重要分支，被广泛应用于无穷组合论、拓扑学、描述集合论等数学分支中的相容性证明中，延森(R.Jensen)于20世纪70年代发展了他的精细结构理论(fine-structure theory)，延森的可构造域的覆盖定理，是20世纪70年代集合论中最引人注目的、最深刻的进展，如今，研究满足很强的大基数假设又具有某种覆盖性质的内模型，成了现代集合论中最富挑战性和最深刻的课题2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学