[科普中国]-富比尼逐项微分定理

富比尼逐项微分定理是有关级数逐项微分的定理。这是由富比尼(Fubini,G.)于1915年得到的。

简介富比尼逐项微分定理是有关级数逐项微分的定理。

这是由富比尼(Fubini,G.)于1915年得到的。

定理若{fn(x)}是区间[a,b]上一列不减（或不增）的函数，使得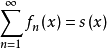在[a,b]上处处存在且有限，则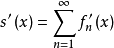几乎处处收敛于[a,b]。

此定理中的fn(x)的条件明显可改为增函数之和，但不可改为增函数之差（有界变差函数）。1

提出者背景富比尼是意大利多产的数学家之一，论述涉及几乎所有数学分支，出版了有关线性微分方程、偏微分方程、多复变解析函数和单调函数等方面的专著；研究过变分学、积分化简、概率分析和函数级数等问题；建立了判定连续群的准则；对非欧几何和微分几何中的许多问题均有论述。

1919年获王室授予的奖金。1928年起，任《纯粹与应用数学年刊》编辑。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学