[科普中国]-中序遍历

中序遍历（LDR）是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。

定义中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。若二叉树为空则结束返回，否则：

（1）中序遍历左子树

（2）访问根结点

（3）中序遍历右子树

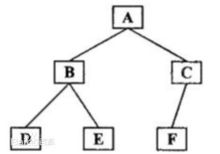
如右图所示二叉树，中序遍历结果：DBEAFC

数学表达式形式当对一棵数学表达式树进行中序，前序和后序遍历时，就分别得到表达式的中缀、前缀和后缀形式。中缀（infix）形式即平时所书写的数学表达式形式，在这种形式中，每个二元操作符（也就是有两个操作数的操作符）出现在左操作数之后，右操作数之前。在使用中缀形式时，可能会产生一些歧义。例如，x+y ×z可以理解为(x+y) ×z或x+ (y ×z)。为了避免这种歧义，可对操作符赋于优先级并采用优先级规则来分析中缀表达式。在完全括号化的中缀表达式中，每个操作符和相应的操作数都用一对括号括起来。更甚者把操作符的每个操作数也都用一对括号括起来。如( (x) + (y) )，( (x) + ( (y) * (z) ) )和( ( (x) + (y) ) * ( (y) + (z) ) ) * (w)。1

复杂性设二叉树中元素数目为n，中序遍历算法的空间复杂性均为O (n)，时间复杂性为(n)。

当t的高度为n时(右斜二叉树的情况)，通过观察其前序、中序和后序遍历时所使用的递归栈空间即可得到上述结论。1

程序实现c++版本树中节点结构为：

typedef struct TreeNode { int data; struct TreeNode *left; struct TreeNode *right; struct TreeNode *parent;} TreeNode;void middle_order(TreeNode *Node) { if(Node != NULL) { middle_order(Node->left); printf("%d ", Node->data); middle_order(Node->right); }}调用时： middle_order(Root); //Root为树的根Java版本class TreeNode{ public int data; public TreeNode leftChild; public TreeNode rightChild; public static void inOrderTraversal(TreeNode node){ if(node == null){ return; }else{ inOrderTraversal(node.leftChild); System.out.println(node.data); inOrderTRaversal(node.rightChild); } }}C#版本/*public class BTNode //二叉树节点类型{ public BTNode lchild; public BTNode rchild; public char data;}*//*public string btstr //全局变量*/public string InOrder(BTNode t){ btstr=""; InOrder1(r); returen btstr;}public string InOrder1(BTNode t){ if(t!=null) { InOrder(t.lchild); bster+=t.data.ToString()+" "; InOrder(t.rchild); }}pascal版本核心代码：

procedure mid(bt:tree);begin if btnil then begin mid (bt^.left); write(bt^.data); mid (bt^.right); end;end;本词条内容贡献者为:

王伟 - 副教授 - 上海交通大学