[科普中国]-谢尔品斯依测度覆盖定理

谢尔品斯基依测度覆盖定理陈述了在一定条件下，直线上的有界点集，近于被有限个互不重叠的区间覆盖的命题。这是谢尔品斯基(Sierpinski,W.)于1923年得到的。

简介谢尔品斯基依测度覆盖定理陈述了在一定条件下，直线上的有界点集，近于被有限个互不重叠的区间覆盖的命题。

这是谢尔品斯基(Sierpinski,W.)于1923年得到的。1

定理设集M⊂(a,b)，△是一区间族。若M中任一点必为△中某一区间的左端点，则对于任给ε>0，△中有不相重叠的有限个区间I1,I2,...,IN适合

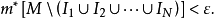
提出者简介谢尔品斯基是波兰数学家，生于华沙，卒于华沙。早年他在华沙大学学习，是沃罗诺伊的学生。

谢尔品斯基是荷兰、捷克斯洛伐克等多个外国科学院的院士，并得到阿姆斯特丹大学、巴黎大学和布拉格大学等多所学校的名誉学位。谢尔品斯基是波兰数学学派的创始人之一曾参与创办了《数学基础》杂志。他的主要贡献在集合论、数论、拓扑学和实变函数论方面。他一生共发表论著700多篇（部），有《连续统假设》(1934)，《关于方程的整数解》(1961)，《初等数论》(1964)等。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学