[科普中国]-椭圆柱坐标系

椭圆柱坐标系（英语：Elliptic cylindrical coordinates）是一种三维正交坐标系 。往 z-轴方向延伸二维的椭圆坐标系，则可得到椭圆柱坐标系；其坐标曲面是共焦的椭圆柱面与双曲柱面。

基本定义椭圆柱坐标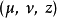 最常见的定义是12

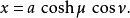
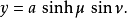
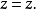其中，实数a>0 ，实数 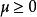，弧度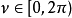 ，坐标 z 是实数。

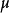的等值曲线形成了椭圆，而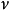的等值曲线则形成了双曲线：

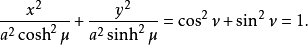
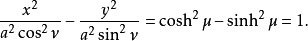
标度因子椭圆柱坐标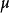与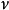 的标度因子相等：

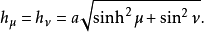
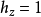
所以，无穷小体积元素等于

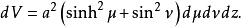
拉普拉斯算子是

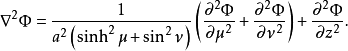
其它微分算子，例如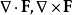，都可以用椭圆柱坐标表达，只需要将标度因子代入正交坐标条目内对应的一般公式。

应用椭圆柱坐标最经典的用途是在解析像拉普拉斯方程或亥姆霍兹方程这类的偏微分方程式。在这些方程式里，椭圆柱坐标允许分离变数法的使用。举一个典型的例题，有一块宽度为{\displaystyle 2a}的平板导体，请问其周围的电场为什么？应用椭圆柱坐标，我们可以有条不紊地分析这例题。

三维的波方程，假若用椭圆柱坐标来表达，则可以用分离变数法解析，形成了马蒂厄微分方程(Mathieu differential equation) 。

参阅拉普拉斯-龙格-冷次向量

本词条内容贡献者为:

杨明 - 副教授 - 西南大学