[科普中国]-最短路径快速算法

最短路径快速算法（英语：Shortest Path Faster Algorithm , SPFA)）是一个用于求解有向带权图单源最短路径的改良的贝尔曼-福特算法。这一算法被认为在随机的稀疏图上表现出色，并且极其适合带有负边权的图。然而SPFA在最坏情况的时间复杂度与贝尔曼-福特算法相同，因此在非负边权的图中仍然最好使用戴克斯特拉算法。SPFA算法是在1994年由段凡丁发表的1。

算法给定一个有向带权图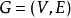 和一个源点 ，SPFA算法计算从 到图中每个节点 的最短路径。对于每个节点 ，从 到 的最短路径表示为 。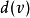

SPFA算法的基本思路与贝尔曼-福特算法相同，即每个节点都被用作用于松弛其相邻节点的备选节点。相较于贝尔曼-福特算法，SPFA算法的提升在于它并不盲目尝试所有节点，而是维护一个备选节点队列，并且仅有节点被松弛后才会放入队列中。整个流程不断重复直至没有节点可以被松弛。

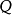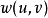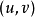下面是这个算法的伪代码。这里的 是一个备选节点的先进先出队列， 是边 的权。

procedure Shortest-Path-Faster-Algorithm(G, s) 1 for each vertex v ≠ s in V(G) 2 d(v) := ∞ 3 d(s) := 0 4 offer s into Q 5 while Q is not empty 6 u := poll Q 7 for each edge (u, v) in E(G) 8 if d(u) + w(u, v)