[科普中国]-最小方差无偏估计

统计学上， 最小方差无偏估计（minimum-variance unbiased estimator，简写为MVUE）是一个对于所有无偏估计中，拥有最小方差的无偏估计。若无论真实参数值θ是多少，最小方差无偏估计（MVUE）都比其他不偏估计有更小或至多相等的方差，则称此估计为一致最小方差无偏估计（uniformly minimum-variance unbiased estimator，简写为UMVUE）。1

原理介绍若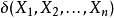为参数函数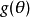的一个无偏估计，且对于参数函数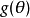的任一无偏估计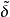恒有下列关系

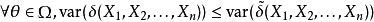
则称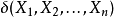为参数函数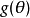的一致最小方差无偏估计（UMVUE）。

若参数函数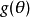存在无偏估计，则可证明出一致最小方差无偏估计存在且只有一个。

一般地，设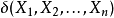是参数函数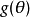的无偏估计且统计量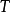是分布族的完备充分统计量，则

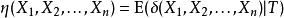
是参数函数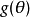的一致最小方差无偏估计（UMVUE）。

评估器选择不需要存在有效的估计量，但如果确实如此，并且如果它是无偏的，那么它就是MVUE。 由于估计量δ的均方误差（MSE）是

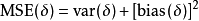
MVUE使无偏估计中的MSE最小化。 在某些情况下，偏差估计量的MSE较低，因为它们的方差小于任何无偏估计量。

例子考虑将数据作为单个观察，来自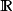上具有密度的绝对连续分布

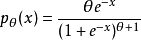
我们希望找到UMVU的估算器

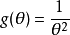
首先，我们了解到密度可以写成

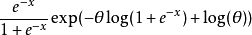
这是一个指数族，具有足够的统计量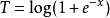。实际上这是一个满秩指数族，因此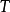足够完整。

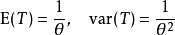
因此，

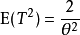
在这里，我们使用Lehmann-Scheffé定理得到MVUE

显然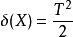是无偏并且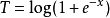足够完整，因此UMVU估算器是

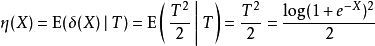
这个例子说明了完整的充分统计量的无偏函数将是UMVU，正如Lehmann-Scheffé定理所述。2

其它例子对于具有未知均值和方差的正态分布，样本均值和（无偏）样本方差是总体均值和总体方差的MVUE。

然而，样本标准偏差对于总体标准偏差不是无偏的。

此外，对于其他分布，样本均值和样本方差通常不是MVUE - 对于具有未知上限和下限的均匀分布，中间范围是总体均值的MVUE。

如果在具有未知上限N的集合{1,2，...，N}上从离散均匀分布中选择k个样本（没有替换），则N的MVUE是

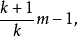
其中m是样本最大值。 这是样本最大值的缩放和移位（如此无偏）变换，这是一个足够和完整的统计量。

本词条内容贡献者为:

王伟 - 副教授 - 上海交通大学