[科普中国]-离散分数傅里叶转换

离散分数傅里叶变换是用来解决数字序列分数傅里叶变换的计算问题，方法是利用它们的特征函数展开的表达来实现离散算法。

背景在建立离散分数傅里叶变换的算法之前，必须对离散傅里叶变换（Discrete Fourier Transform）有一定的理论认识。对于一般的傅里叶变换具有4周期性质，也就是对任何信号连续做4次傅里叶变换就会回到它自己。离散傅里叶变换也有这样的性质1。

对于一串数字序列信号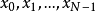，定义它的离散傅里叶变换是：

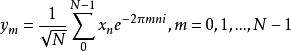
定义离散分数傅里叶变换是用来解决数字序列分数傅里叶变换的计算问题，方法是利用它们的特征函数展开的表达来实现离散算法，而离散分数傅里叶变换的特征函数是埃尔米特多项式与高斯函数的乘积，这样的特征函数同时也是傅里叶变换的特征函数。利用离散傅里叶变换的结果，可以建立周期分数傅里叶变换的离散算法2。

计算方法根据离散傅里叶变换的矩阵形式，定义符号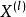：，其定义如下：

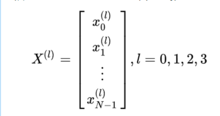
其递回关系为：

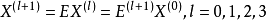
当 l=0 时，对应的是原始数字序列信号；当 l=1时，对应的昰原始数字序列信号的离散傅里叶变换。现在定义幂次a的离散分数傅里叶变换为：

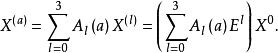
上式中的 A是a的连续函数。引入矩阵符号为：

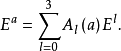
称作矩阵E的a次幂，因此幂次a的离散分数傅里叶变换可以写成：

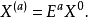
本词条内容贡献者为:

何星 - 副教授 - 上海交通大学