[科普中国]-香农-范诺编码

在数据压缩的领域里，香农-范诺编码（Shannon–Fano coding）是一种基于一组符号集及其出现的或然率（估量或测量所得），从而构建前缀码的技术。

简介香农-范诺编码其名称来自于以克劳德·香农和罗伯特·法诺。在理想意义上，它与哈夫曼编码一样，并未实现码词（code word）长度的最低预期;然而，与哈夫曼编码不同的是，它确保了所有的码词长度在一个理想的理论范围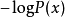 之内。这项技术是香农于1948年，在他介绍信息理论的文章“通信数学理论”中被提出的。这个方法归功于范诺，他在不久以后以技术报告发布了它。香农-范诺编码不应该与香农编码混淆，后者的编码方法用于证明Shannon's noiseless coding theorem，或与Shannon–Fano–Elias coding（又被称作Elias coding）一起，被看做算术编码的先驱1。

香农-范诺编码，符号从最大可能到最少可能排序，将排列好的信源符号分化为两大组，使两组的概率和近于相同，并各赋予一个二元码符号“0”和“1”。只要有符号剩余，以同样的过程重复这些集合以此确定这些代码的连续编码数字。依次下去，直至每一组的只剩下一个信源符号为止。当一组已经降低到一个符号，显然，这意味着符号的代码是完整的，不会形成任何其他符号的代码前缀。

这是一个行之有效的算法，它会产生相当有效的可变长度编码;当两个较小的集生产分区其实是相等的概率，一位用于区分它们的信息是最有效的使用。不幸的是，香农 - 法诺并不总是产生最优的前缀码：概率{0.35，0.17，0.17，0.16，0.15}是一个将分配非优化代码的Shannon-Fano的编码的一个例子。

出于这个原因，香农 - 范诺几乎从不使用; 哈夫曼编码几乎是计算简单，生产总是达到预期最低的码字长度的制约下，每个符号是由一个整数组成一个代码代表的前缀码。这往往是不必要的，因为代码将装在首尾相连的长序列的里。如果我们认为一次的代码组，象征符号的哈夫曼编码是最佳符号的概率统计独立|独立和一些半功率，即，为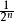 。在大多数情况下，算术编码可以产生比哈夫曼或的香农-范诺更大的整体压缩，因为它可以在小数位编码，这更接近实际的符号信息内容。然而，算术编码并没有取代像霍夫曼取代的香农-范诺一样取代哈夫曼，一方面是因为算术编码的计算成本的方式，因为它是由多个专利覆盖。香农：范诺编码被用在爆聚压缩方法。

香农-范诺算法Shannon-Fano的树是根据旨在定义一个有效的代码表的规范而建立的。实际的算法很简单：

对于一个给定的符号列表，制定了概率相应的列表或频率计数，使每个符号的相对发生频率是已知。

排序根据频率的符号列表，最常出现的符号在左边，最少出现的符号在右边。

清单分为两部分，使左边部分的总频率和尽可能接近右边部分的总频率和。

该列表的左半边分配二进制数字0，右半边是分配的数字1。这意味着，在第一半符号代都是将所有从0开始，第二半的代码都从1开始。

对左、右半部分递归应用步骤3和4，细分群体，并添加位的代码，直到每个符号已成为一个相应的代码树的叶。

示例这个例子展示了一组字母的香农编码结构（如图a所示）这五个可被编码的字母有如下出现次数：

|| ||

从左到右，所有的符号以它们出现的次数划分。在字母B与C之间划定分割线，得到了左右两组，总次数分别为22,17。这样就把两组的差别降到最小。通过这样的分割, A与B同时拥有了一个以0为开头的码字, C，D，E的码子则为1,如图b所示。随后，在树的左半边，于A，B间建立新的分割线，这样A就成为了码字为00的叶子节点，B的码子01。经过四次分割，得到了一个树形编码。如下表所示，在最终得到的树中，拥有最大频率的符号被两位编码，其他两个频率较低的符号被三位编码。

|| ||

根据A，B，C两位编码长度，D，E的三位编码长度，最终的平均码字长度是

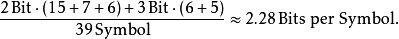
本词条内容贡献者为:

王伟 - 副教授 - 上海交通大学