[科普中国]-最小圆覆盖算法

最小圆覆盖是数学中的一个算法问题，研究如何寻找能够覆盖平面上一群点的最小圆。这个问题在一般的n维空间中的推广是最小包围球的问题，即寻找能覆盖n维空间中某个点集的最小球。最小圆覆盖问题最早由十九世纪的英国数学家詹姆斯·约瑟夫·西尔维斯特在1857年提出。1

最小圆覆盖也是运筹学中设施选址问题的一种。广义的设施选址问题研究的是当已知一些目标点（仓库、销售终端、供应商等等）的位置时，求满足与这些目标点的距离相关的点的某些极值。最小圆覆盖可以看作是研究“到一些点的距离之最大值最小的点”的问题。现有的算法可以在线性时间内计算最小圆覆盖或最小包围球的问题。

算法描述寻找最小覆盖圆的大部分几何方法都是寻找给定点集中经过最小覆盖圆的那些点。这是基于以下两个事实：

最小覆盖圆是唯一存在的。

给定的点集中，最多有三个点在最小覆盖圆上。如果有三个点在最小覆盖圆上，那么最小覆盖圆就是这三点的外接圆；如果只有两个点在最小覆盖圆上，那么最小覆盖圆就是以这两点之间的直线段为直径的圆。

线性时间解决方案正如Nimrod Megiddo所示，最小包围圆可以在线性时间内找到，并且相同的线性时间界限也适用于任何常数维的欧几里德空间中的最小包围球。

Emo Welzl 基于Raimund Seidel的线性规划算法，提出了一种在预期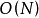 时间内运行的最小覆盖圆问题的简单随机算法。 该算法如下所示。

随后，最小圆问题被包含在一类普通的LP类型问题中，这些问题可以通过像Welzl基于线性规划的算法来解决。 作为该类成员的结果，表明在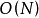 时间界限中对常数因子的维度的依赖性，这是Seidel方法的因子，可以减少到亚指数，但仍然只保持对 的线性依赖。2

Welzl的算法该算法是递归的，并且将两个（有限的）点P和R作为参数;它计算P和R联合的最小包围圆，只要R的每个点都是最终最小包围圆的边界点之一。因此，原始的最小包围圆问题可以通过调用算法来解决，其中P等于要封闭的点集合，R等于空集合;当算法递归调用自身时，它将放大传递给递归调用的集合R，直到它包含圆的所有边界点。
该算法以随机顺序处理P的点，保持处理点的集合S和包含并集S∪R的最小圆D.在每一步，它测试下一个要处理的点p是否是在D;如果不是，该算法用集合S和R∪p上的算法的递归调用的结果替换D.无论圆是否被替换，p都被包括在集合S中。因此，处理每个点包括在恒定时间内测试该点是否属于单个圆并且可能执行对算法的递归调用。可以看出，总时间是线性的。

algorithm welzl: input: Finite sets P and R of points in the plane output: Minimal disk enclosing P with R on the boundary, or undefined if no such disk exists if P is empty or |R| ≥ 3: if |R| = 1: (we do this to support multisets with duplicate points) (we assume that a circle with a radius of zero can exist) p := R[0] return circle(p, 0) else if |R| = 2: (we do this to support multisets with duplicate points) (we use that the smallest circle between two points has a center at their midpoint) (and the segment that passes through them is a diameter of the circle) p0 := R[0] p1 := R[1] center := midpoint(p0, p1) diameter := distance(p0, p1) return circle(center, diameter / 2) else if the points of R are cocircular: return the ball they determine else: return undefined choose p in P (randomly and uniformly) D := welzl(P - { p }, R) if p is in D: return D return welzl(P - { p }, R ∪ { p })其它算法在Megiddo的结果显示最小圆问题可以在线性时间内解决之前，文献中出现了几种更高复杂度的算法。一个朴素的算法通过测试由所有对和三元组确定的圆来解决时间O（n4）中的问题。

Chrystal和Peirce算法应用局部优化策略，该策略在包围圆的边界上保持两个点并反复收缩圆，替换该对边界点，直到找到最佳圆。 Chakraborty和Chaudhuri [9]提出了一种线性时间方法，用于在该圆上选择合适的初始圆和一对边界点。算法的每个步骤包括作为两个边界点之一的凸包的新顶点，因此如果船体具有h个顶点，则该方法可以实现为在时间O（nh）中运行。

Elzinga和Hearn [10]描述了一种算法，该算法为点的子集保持覆盖圆。在每个步骤中，当前球体未覆盖的点用于查找覆盖新的点子集的较大球体，包括找到的点。尽管其最差的运行时间是O（h3n），但作者报告说它在实验中以线性时间运行。 Drezner和Shelah分析了该方法的复杂性。Fortran和C代码均可从Hearn，Vijay&Nickel（1995）获得。

最小的球体问题可以表示为由具有凸二次目标函数的线性约束系统定义的二次程序[1]。因此，任何可行的方向算法都可以解决问题。Hearn和Vijay证明Jacobsen选择的可行方向方法等同于Chrystal-Peirce算法。

这个二次规划的对偶也可以明确地表达出来; Lawson 的算法可以用这种方式描述为原始对偶算法。

Shamos和Hoey基于观察得到了问题的O（n log n）时间算法，即最小包围圆的中心必须是输入点集的最远点Voronoi图的顶点。

本词条内容贡献者为:

王伟 - 副教授 - 上海交通大学