[科普中国]-演算式微分

在数学和计算机代数中，演算式微分有时称作自动微分，是一种可以借由计算机程序计算一个函数导数的方法。两种传统做微分的方法为：

1）对一个函数的表示式做符号上的微分，并且计算其在某一点上的值。

2）使用差分。

使用符号微分最主要的缺点是速度慢及将计算机程序转换成表示式的困难。此外，很多函数在要计算更高阶微分时会变得复杂。 使用差分的两个重要的缺点是舍弃误差及数值化过程和相消误差。此两者传统方法在计算更高阶微分时，都有复杂度及误差增加的问题。自动微分则解决上述的问题。

复合函数求导法则，前向和反向积累自动微分的基础是，根据复合函数求导法则来合并微分值。以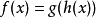为例，根据复合函数求导法则，我们有1：

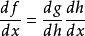
通常有两个不同的模式：“前向积累”（或“前向模式”）和“反向积累”（或反向模式）。 前向积累由右到左地使用复合函数求导法则，即先计算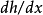 ，然后才。 反向积累则是由左到右。

应用前向式积累是由对程式的非标准化转译程序来实作。 即将实数替换成二元数，常数则换成有第二项为零系数的二元数。 而数值上基本运算则被换成二元数的运算。 非标准化转译程序一般使用两者策略之一：程式码转换和运算符重载。

程式码转换一个函数的程式码会被自动产生的程式码所替换， 新生成用来计算导数的程式码则会插入原程式码中。

程式码转换可实作在所有的编程语言上，且它对编译器而言，是容易最佳化的。 然而，实作自动微分的工具则是比较困难的。

运算符重载如果所使用的编程语言支持，运算符重载是个可行的方法。 实数的物件跟基本数学运算必须重载以满足上述 augmented 算术。 这不须要改变要被微分的函数的程式码。

运算符重载对前向积累是容易实作的，并且可能对反向积累亦如此。 然而，与前向积累相比，现有的编译器在最佳化程式码方面则是较为落后。

本词条内容贡献者为:

王伟 - 副教授 - 上海交通大学