[科普中国]-连锁推理

连锁推理(sorites)是复合三段论的省略形式之一，它在一个复合三段论中，只提出最后一个总的结论，而省略其他各三段论的结论，与复合三段论相应，它也有两种形式1。

基本介绍连锁推理又名 “连锁三段论”，是复合推理的省略形式，即在复合三段论中，只保留最后一个三段论的结论，其余各个三段论的结论都被省略的推理。与复合推理的两种形式相适应，连锁推理也可分为前进的连锁推理和后退的连锁推理。

前进的连锁推理是前进的复合推理的省略式。它只保留了最后一个三段论的结论，而省略了其他各个三段论的结论。其结构形式是： D是E，C是D，B是 C，A是B，所以，A是E。在这形式中省略了中间结论“C是E”和 “B是E”。

后退的连锁推理是后退的复合推理的省略形式，它保留最后 一个三段论的结论，而省略了其他各个三段论的结论。其结构形式是：“A是B，B是C，C是D，D是E，所以，A是E。”在这一形式中，“A是C”、“A是D”等都被省略 了。在前进的连锁推理中，被省略的 这些判断既是前一三段论的结论，又是后一三段论的大前提。在后退的连锁推理中，被省略的这些判断既是前 一三段论的结论，又是后一三段论的小前提。

前进连锁推理前进连锁推理即前进的连锁三段论，即在前进的复合三段论中，只提出最后一个结论，而省略其余各个三段论的结论。由于这种形式是由德国的哥克兰尼(Rodolphus Goclenius，1547—1628)所提出的，故亦称哥克兰尼式连锁三段论。例如：“凡以种子繁殖的植物(M1)，都是高等植物(P)，裸子植物(M2)是以种子繁殖的植物(M1)，银杏目植物(M3)是裸子植物(M2)，银杏(S)是银杏目植物(M3)，所以，银杏(S)是高等植物(P)。”其逻辑形式为2：

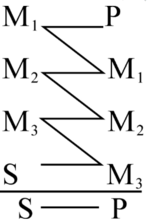
后退连锁推理后退连锁推理即后退的连锁三段论，即在后退的复合三段论中，只提出最后一个结论，而省略其余各个三段论的结论。由于这种形式是由亚里士多德最先提出的，故亦称亚里士多德式连锁三段论。例如：“银杏(S)是银杏目植物(M3)，银杏目植物(M3)是裸子植物(M2)，裸子植物(M2)是以种子繁殖的植物(M1)，以种子繁殖的植物(M1)是高等植物(P)，所以，银杏(S)是高等植物(P)。”其逻辑形式为2：

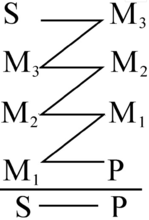
本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学