[科普中国]-亨廷顿公理系统

亨廷顿公理系统(Huntington axiomatic system)通常用来定义布尔代数〈B，+，·，′，0，1〉的一种公理系统，由亨廷顿(E.V.Huntington)于1904年提出，值得指出的是，这个公理系统中每一条都有两个式子，它们互为对偶，因此通常把这些条件称为自对偶的公理系统；然而这个公理系统却不是独立的，若将布尔代数的性质3中a+0=a或a·1=a去掉，则由其余的公理组成的系统才是独立的1。

基本介绍在布尔代数中，有几种不同的公理系统。但是比较简单、方便的，乃是美国数学家亨廷顿(Huntington, E. V., 1874--1952)于1904年提出的公理系统2:

Ⅰ闭合律:对于全部的x, y∈K,有

(1) (x+y)∈K

(2) (x.y)∈K

Ⅱ(1)对于全部的x∈K,存在着元素0∈K,它能使x+0=x

(2)对于全部的x∈K，存在着元素1∈K，它能使x.1=x

Ⅲ 交换律: 对于全部的x, y∈K，有

(1) x+y=y+x

(2) x.y=y.x

Ⅳ分配律:对于全部的x,y, z∈K,有

(1) x+(y.z)= (x+y).(x+z)

(2) x.(y+z)=x·y+x·z

Ⅴ补：对于每个x∈K,存在着,它能使

(1)

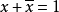
(2)

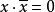
Ⅵ至少存在两个元素x, y∈K,能使x≠y。

把上述公理系统与普通代数中的公理系统加以比较后看出，它们之间有相似之处，也有不同之处。在普通代数中，没有公理Ⅳ(1)中所示的加对乘的分配律,也没有补的概念。

这里着重指出，当K={0,1}时，我们把上述布尔代数叫做二值布尔代数。开关电路中所使用的就是这种二值布尔代数,所以也把它叫做开关代数。此外，因为逻辑命题只有真和假两种可能,而真和假的值可用1和0代表， 所以有时也把二值布尔代数叫做逻辑代数。这些代数都是布尔代数2。

关于亨廷顿公理的讨论下面我们讨论亨廷顿公理本身的问题。

公理是客观存在的抽象，无需证明。但是可以用客观存在来验证。例如我们可以用集合论中的文氏图来验证亨廷顿公理。

杂乱的公理系统是没有用处的。 因此， 要想构成一个有用的公理系统，必须满足三个要求：无矛盾性、独立性和完备性。下面将分别予以讨论2。

公理系统内各条公理之间不应当有矛盾。为了证明亨廷顿公理之间无矛盾性，我们可以逐个地研究每条公理，以便推论出每条公理与共他公理不发生矛盾。然而这样做是非常繁琐的。为了克服这种繁琐的证明， 亨廷顿提出了一个巧妙的数学方法。他说如果我们能找到一个布尔代数的例子，并且已知这个布尔代数是没有矛盾的，那么当这个无矛盾的布尔代数能满足全部字廷顿公理时，亨廷顿公理系统本身就应当没有矛盾性。由0和1两个元素组成的布尔代数，是最简单的布尔代数，并规定

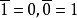
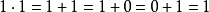且 0+0=0·0=1·0=0·0=0。

现在我们把由0和1组成的布尔代数应用于亨廷顿公理系统。我们将看到，根据对这个布尔代数的规定，能满足各条公理。例如我们先看公理Ⅰ(1)。0,1∈K，则当x=0,y=1时，

0+1=1∈K，

而当x=1，y=0时，

1+0=1∈K，

所以由0和1组成的布尔代数能满足公理Ⅰ(1)。类似地，也能满足公理Ⅰ(2)。

再看公理Ⅱ(1)。 如果x= 1,我们有

x+0=1+0=1，

如果x=0，则

x+0=0+0=0，

类似地，也能满足公理Ⅱ(2)。

再看公理Ⅲ(1)。我们首先列出x，y的值的各种可能组合，并列出各种组合时的x+y和y+x,如图1所示。这个表叫做公理Ⅲ(1)的真值表。由表中看出,x+y和y+ x这两列的值是相等的。于是由0和l组成的布尔代数能满足公理Ⅲ(1)。类似地，也可满足公理Ⅲ(2)2。

用类似的方法，还可证明由0和1组成的布尔代数能满足其他各条公理。读者不妨一试。

现在我们讨论公理的独立性。所谓公理的独立性，是指任何一条公理均不能由另一条公理所证明，也就是说，在公理系统中没有多余的公理。上述亨廷顿公理系统是独立的。证明公理的独立性这里不再讨论。

这里需要指出，尽管我们要求公理系统是独立的，但是非独立的公理系统无损于公理系统的正确性。事实上，有些作者就采用了非独立公理系统。这种系统的优点是利用多余的公理便于推导定理和导出公式。但是采用独立的公理系统，却有助于提高读者运算布尔代数的能力。

所谓公理系统的完备性，是说所有的定理都可以由该公理系统推导出来。稍后，我们将利用公理推导定理。在此之前，我们研兖公理系统中一种有趣的性质，即所谓对偶性2。

亨廷顿公理是成对地提出的。我们发现，如果把公理系统中的“+”换成“·”，而把“·”换成“+”,并且把0换成1,而把1换成0,则一对公理中的一个公理可变换成另一个公理。这种性质叫做对偶性。例如

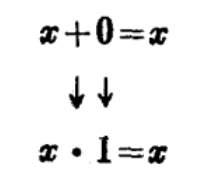
又如

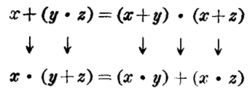
本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学