[科普中国]-单元集

单元集(singleton)又称“单元素集”，是只有一个元素的集合。它的基本形式是{a}，其中a是其唯一的元素。

基本介绍单元集亦称单元素、单元素集，是一种特殊的集合，即只含有一个元素的集合。元素a组成的单元集记为{a}。单元集可看成是无序对集合的特例，即1

无序对集合简称无序对，又称无序偶，是一种特殊的集合，即仅含两个元素的集合。对于任意的两个对象(集合)u与v，集合{u，v}={v，u}称为对象u与v的无序对，由于u，v是任意的两个对象，u与v既可以相同也可以不同，当u=v时，{u，v}可以记为{u}或{v}，集合{u}或{v}称为单元集，即仅含有一个元素的集合，故单元集是无序对集合的一种特殊情况1。

相关概念无论是在数学活动中。还是在日常生活中，我们都曾不止一次地使用过“集合”一词，例如，“小于5的自然数构成的集合”、“某一平面内的所有三角形组成的集合”、“中国的直辖市组成的集合”、“济源市图书馆的全部藏书组成的集合”等2。

一般地，我们把具有确定性质而相互间又有明确区别的一些对象的全体称为集合，简称为集，集合中的每个对象叫作这个集合的元素。

例如，某职业技术学院的全体学生组成一个集合．每个学生都是这个集合的元素；某企业生产的一批电视机(每个个体都被看作是不同的)组成一个集合，其中的任何一台电视机都是这一集合的元素；太阳系的所有行星组成一个集合，每个行星都是这个集合的元素。

通常用大写字母表示集合，用小写字母表示元素。例如，常用的一些数集(元素为数的集合)通常用如下字母表示：N表示自然数集，Z表示整数集，Q表示有理数集，R表示实数集。如果上述数集中的元素只限于正数，就在集合记号的右上角标上“+”号；如果数集中的元素都是负数，就在集合记号的右上角标上“-”号。例如，正整数集用N-表示。负整数集用Z-表示，正实数集用R+表示等。

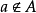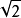若a是集合A的元素，就说“属于A，记作“a∈A”；若a不是集合A的元素，就说a不属于A，记作“”。例如0∈N，-1N，-2∈Z，∈R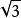，Q，π∈R等，可见数学符号“∈”与“”用来表示元素与集合之间的关系。

包含有限个元素的集合称为有限集，不是有限集的集合称为无限集。例如，“我国985”某班级学生组成的集合”都是有限集，而自然数集、整数集、有理数集和实数集都是无限集。

我们把不含有任何元素的集合叫作空集，记作“∅”，读作“欧”。空集是唯一的，空集是有限集。例如，“方程线x2+1=0在实数范围内的解集”就是空集，我们把至少含有一个元素的集合叫作非空集2。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学