[科普中国]-典型格

典型格即三段论的第一格，亦称公理格、完全格、标准格、完善格等，是三段论的一种格式，指中项是大前提的主项、小前提的谓项的一种三段论形式。第一格的特殊规则如下：1.大前提必须是全称的；2.小前提必须是肯定的。在大前提中指出了关于一类情况，在小前提中把某些事物归到这一类中，因而得出关于某些事物情况的结论，三段论第一格明显、自然地表现了演绎推理由一般到特殊的思维过程，它是三段论中最基本的形式，这一格因此又称为完善格1。

基本介绍典型格即三段论的第一格，简称“第一格”。中项在大前提中为主项，在小前提中为谓项的三段论形式。其结构是：

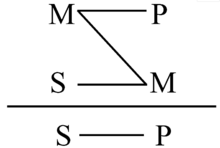
例如：

又如“凡真理是不怕批评的，马克思主义是真理，所以马克思主义是不怕批评的2。

典型格的特殊规则”运用三段论第一格进行推理时，要遵守以下两条特殊规则：

(1)小前提必须是肯定命题。

(2)大前提必须是全称命题;

证明：小前提必须肯定。假设如果小前提是否定的，则结论否定，根据是规则(5)（前提中有一个是否定的，则结论必然是否定的）;如果小前提是否定的，则大前提必须肯定，根据是规则(4)（两个否定前提不能得出必然结论）；结论否定，说明大项在结论中是周延的；大前提肯定，说明大项在前提中是不周延的。这说明，如果小前提否定，就会导致“大项扩大”的逻辑错误，因此，小前提必须肯定。

大前提必须全称。由于小前提必须肯定，因此，处在小前提谓项位置的中项是不周延的，但中项在前提中至少应周延一次，根据是规则(2)（中项在前提中至少周延一次）。要使处在大前提主项位置的中项周延，大前提必须全称3。

典型格的特点典型格的特点是：大前提是关于一类事物的断定，小前提肯定某些事物属于这一类事物，因此可推出关于某些事物情况的结论3。三段论的第一格典型地体现了演绎推理由一般到特殊的思维进程，它的AAA式和EAE式又直接体现了三段论的公理，并且在三段论的四个格中，只有第一格才能推出直言命题的四种形式：A、E、I、O，而且也只有第一格才能推出全称肯定命题(A)，故亚里士多德称之为“完善的格”，传统逻辑也称之为“典型格”。三段论第一格在人们认识和思维中的主要作用，在于把一般原理、原则的知识运用于分析和说明特殊事实，以获得关于特殊事实的某种必然性结论或用于论证关于某种特殊事实的命题的真实性2。

典型格的用途典型格具有广泛的用途，其主要作用是根据一般来认识特殊，在思维过程中，当人们需要根据一般性原理做出特殊性结论的时候，常常使用第一格。第一格在司法工作中有着特殊的作用，因此第一格也叫“审判格”。

例如：

所有贪污公款的行为，都要受到法律的制裁，

某人贪污公款，

所以，某人要受到法律的制裁。3

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学