[科普中国]-归谬式推理

归谬式推理(inference with absurdity)是一种间接推理，是由两个前件相同，后件相矛盾的充分条件假言命题为前提，从而推出与这两个假言命题的前件相矛盾的命题的推理。例如：如果一切判断都是假的，则世界上没有真的判断；如果一切判断都是假的，则世界上没有真的判断也假，所以，并非一切判断都是假的1。

基本概念归谬式推理(inference with absurdity)是这样一种推理，它的前提是两个充分条件假言判断，其前件相同，后件相矛盾，而结论是与这两个假言判断的前件相矛盾的判断。例如：

如果大前提特称，小前提否定能得出结论，那么大前提中的大项应该周延；

如果大前提特称，小前提否定能得出结论，那么大前提中的大项不能周延；

所以，大前提特称，小前提否定不能得出结论2。

归谬式推理的逻辑形式归谬式推理的逻辑形式表示如下2：

如果p，那么q

如果p，那么非q

所以，非p

或用公式表示为：

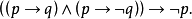
或者3

如果非p，那么q

如果非p，那么非q

所以，p。

归谬式推理的应用与举例归谬式推理形式在论证中经常使用，当我们反驳某一判断时，可以先假设这个判断是真的，并从这种假设中同时引伸出两个相矛盾的判断，再从这两个判断的矛盾性推出被反驳的判断必然是假的。比如，有人认为“一切判断都是假的”。我们就可以用归谬式推理来驳斥他，先假设这个判断是真的，即如果“一切判断是假的”这一判断是真的，那么“一切判断都是假的”；如果“一切判断都是假的”这一判断是真的，那么“并非一切判断都是假的”(有的判断不是假的)，所以，“一切判断都是假的”不是真的2

【例1】如果张三作案，那么李四一定是主犯；如果张三没作案，那么王五参与作案。如果李四不是主犯，那么王五没有参与作案3。

由此可推出以下哪项?

A．张三没作案

B．李四一定是主犯

C．李四不一定是主犯

D．王五参与作案

E．张三作案

解析：

首先把题干中第一句话“如果张三作案，那么李四一定是主犯”变为：“如果李四不是主犯，那么张三没作案”；再与题干中的第二句话“如果张三没作案，那么王五参与作案”进行推理得：“如果李四不是主犯，那么王五参与作案”；这样与第三句话：“如果李四不是主犯，那么王五没有参与作案”构成归谬式推理，即：

如果李四不是主犯，那么王五参与作案，

如果李四不是主犯，那么王五没有参与作案，

所以，李四是主犯3。

【例2】意大利物理学家伽利略推翻古代“物体下落速度与重量成正比”(p)这一错误理论时运用的就是归谬式推理。伽利略设计了一个实验：A、B两块石头，并且A重于B，把A、B两块石头捆在一起，据此进行推导：

如果p成立。因A+B比A重，那么，A+B的下落速度比A快(用q表示)；

如果p成立，因速度小的B加在速度大的A上会减低A的速度，

那么，A+B的下落速度比A慢(这就是非q)；

所以，p不成立。(即“物体下落速度与重量成正比”这一理论是错误的)4。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学