[科普中国]-闭系统定律

闭系统定律(law of a closed system)亦称豪伯定律、闭语句定理，数学中的重要定理，即对于构成一个闭系统的n个命题：如Ai成立则Bi(i=1，2，…，n)成立，则当Bi成立时Ai(i=1，2，…，n)也成立。

基本介绍在数学证明中，原命题和逆命题的关系是重要的，一般由原命题为真不足以断定其逆命题为真，但是在逻辑学中有一个闭系统定律(又名豪伯定律)，从满足一定条件的n个原命题为真，即可得到其相应的n个逆命题也为真1。

闭系统与闭系统定律 如果n个原命题具有下述形式：

(1)如果A₁，则B₁；

(2)如果A₂，则B₂；

(3)如果A₃，则B₃，

并且A₁，A₂，…，An包括了所论问题所有的可能性，B₁，B₂，…，Bn互相排斥，此时称这n个命题构成一个闭系统，则闭系统定律断定，在这n个命题为真时，其相应的n个逆命题：

(1’)如果B₁，则A₁；

(2’)如果B₂，则A₂；

(3')如果B₃，则A₃

也为真1。

闭系统定律的证明下面我们只证明(1')为真，即如果B₁为真，则A₁为真。

如果A₁不真，则因为A₁，A₂，…，An包括了所有的可能性，即

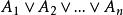为真，故必有Ai(i≠1)为真，又由于命题(i)为真，则有Bi(i≠1)为真，但B₁和Bi(i≠1)互斥，所以B₁和Bi不可能同时为真，由这个矛盾就证明了如果B₁为真，则A₁为真。

仿此可证明其余(n-1)个逆命题成立1。

举例分析【例1】在实系数方程ax²+bx+c=0(a≠0)的理论中，命题：

1.如果Δ=b²-4ac>0，则它有两个不相等的实根；

2.如果Δ=b²-4ac=0，则它有两个相等的实根；

3.如果Δ=b²-4ac0；

2.如果它有两个相等的实根，则Δ=b²-4ac=0；

3.如果它无实根，则Δ=b²-4acAC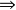 ∠C>∠B;

2.AB=AC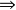 ∠C=∠B;

3.ABAC;

2.∠C=∠B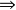 AB=AC;

3.∠C