[科普中国]-纯粹关系推理

纯粹关系推理(pure relational inference)是指前提与结论均为关系命题的关系推理。例如“4=22，所以，22=4”。“长江长于黄河，黄河长于珠江，所以，长江长于珠江”。前者是根据“=”(等于)关系的对称性而进行推演的关系推理，其逻辑形式为：“aRb，所以bRa”；后者是根据“长于”关系的传递性而进行推演的关系推理，其逻辑形式为：“aRb，bRc，所以，aRc”。只要在推理中严格根据关系本身的逻辑性质，纯粹关系推理的结论就是必然推出的1。

基本介绍关系推理有纯粹关系推理和混合关系推理之分。纯粹关系推理是根据关系的性质而由前提必然推出结论的；推理。例如：

①甲案先于乙案发生，

乙案先于丙案发生，

所以，甲案先于丙案发生。

②A命题与B命题具有矛盾关系，

B命题与C命题具有矛盾关系，

所以，A命题与C命题必不具有矛盾关系2。

纯粹关系推理的分类纯粹关系推理根据前提中关系命题的数量，可以分为直接关系推理和间接关系推理。

直接关系推理所谓直接关系推理，就是以一个关系命题为前提，并依据关系的对称性或反对称作，必然推出另一个关系命题为结论的推理。例如2：

③A与B交叉，

所以，B与A交叉。

例③就是一个直接关系推理。它是根据“交叉”这一关系的对称性而推演的，因此，逻辑上称之为对称关系推理。其形式结构为；

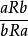或者：

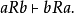又例如：

④A大于B，

所以， B不大于A。

例④也是一个直接关系推理。它是根据“大于”这一关系的反对称性而推演的，因此，逻辑上称之为反对称关系推理。其形式结构为：

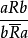或者：

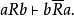
运用直接关系推理时，应注意不要把非对称关系当作关系推理的依据。因为，若根据非对称关系进行推演，其结论就未必可靠，这就违反了必然性推理的逻辑特性。例如：“甲认识乙，所以乙认识甲”这一推理的结论就不具有必然性，把它作为关系推理就是错误的，其原因就是“认识”为非对称关系2。

间接关系推理所谓间接关系推理，就是以两个关系命题为前提，并依据关系的传递陆或反传递性，必然推出另一个关系命题为结论的推理。例如2：

⑤A真包含于B，

B真包含于C，

所以， A真包含于C。

例⑤就是一个间接关系推理，它是根据“真包含于”这二关系的传递性而推演的，因此，逻辑上称之为传递关系推理。其形式结构为：

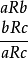或者：

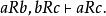又例如：

⑥甲比乙大两岁，

乙比丙大两岁，

所以，并非甲比丙大两岁。

例⑥也是一个间接关系推理。它是根据“…比…大两岁”这一关系的反传递性而推演的，因此，逻辑上称之为反传递关系推理。其形式结构为：

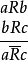或者：

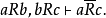
运用间接关系推理时，应注意不要把非传递关系当作关系推理的依据。因为，若根据非传递关系进行推演，其结论未必可靠，这与必然性推理的逻辑特性是相违背的。例如，甲队战胜乙队，乙队战胜丙队，所以，甲队战胜丙队。这推理就不能成立，其原因是“战胜”为非传递性关系2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学