[科普中国]-命题常元

命题常元(propositional constant)亦称命题定元、命题常项、特定的命题，初等代数中的常数或常元在命题代数中的对应概念。在命题代数W中，用一个字母表示W的某个固定的命题，这个字母称为W的常元或定元，如F，T都是命题常元1。

基本概念在命题逻辑中，命题又有命题常元和命题变元之分，一个确定的具体的命题，称为命题常元；一个不确定的泛指的任意命题，称为命题变元，显然，命题变元不是命题，只有用一个特定的命题，即对该命题变元赋值0或1才能确定它的真值。

命题常元和命题变元都用字母p，q，r，…表示，在命题逻辑中我们只关心命题的真值，故给出如下形式的定义。

定义1 以真或1、假或0为其变域的变元，称为命题变元；真或1、假或0称为命题常元。

命题常元、变元及联结词是形式描述命题及其推理的基本语言成分，用它们可以形式地描述更为复杂的命题2。

相关概念及结论定义2 单个命题变元和命题常元称为原子命题公式，简称原子公式2。

定义3 合式公式是由下列规则生成的公式：

①单个原子公式是合式公式。

②若A是一个合式公式，则¬A也是一个合式公式。

③若A、B是合式公式，则A∧B、A∨B、A→B和A↔B都是合式公式。

④只有有限次使用①、②和③生成的公式才是合式公式。

合式公式也称为命题公式或命题形式，简称为公式。

按照上述定义，下面的符号串是公式：

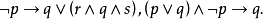下面的符号串不是公式：

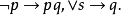
定义3 如果B是公式A中的一部分，且B为公式，则称B是公式A的子公式。

当合式公式比较复杂时，常常使用很多例括号，为了减少圆括号的使用量，可作以下约定：

①规定联结词的优先级由高到低的次序为：¬、∧、∨、→、↔。

②相同的联结词按从左至右次序计算时，圆括号可省略。

③最外层的圆括号可以省略。

对公式中的命题变元各指定一个真值，称为对公式的赋值或解释，若指定的一组值是公式真值为1，称这组值为公式的成真赋值；若指定的一组值是公式真值为0，称这组值为公式的成假赋值。

定义4 对于公式中命题变元的每一种可能的赋值，以及由它们确定出的公式真值所列成的表，称为该公式的真值表。

用归纳法不难证明，对于含有n个命题变元的公式，有2n个赋值，即在该公式的真值表中有2n行。

为方便构造真值表，特约定如下：

①将n个命题变元按字母序或下标序排列，列出2n个赋值，赋值从00…0开始，然后按二进制加法依次写出每个赋值，直到11…1为止。

②若公式较复杂，可先列出各子公式的真值（若有括号，则应从里层向外层展开）。

③最后列出所求公式的真值2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学