[科普中国]-非线性跟车模型

Herman，Rothery、Gazis等人，假定跟车模型中获得性因子与后车的速度成m次幂的正比例关系，与前后车之间的相对距离成l次幂的反比例关系，我们推导出一个非线性的跟车模型，后来有人称它为“L&M模型”。对该方程积分可以产生各种想要的流量/密度方程。

从一般的非线性跟车模型可以看出，滞后时间T（h(t)）实质上是由跟车车辆的车间距h（t）决定的，对于这种表现滞后时间和状态有关的微分系统的特点之一就是有可能出现因果倒置关系的出现，即先输入的信号后有输出，而后输入的信号先有输出。

跟车模型跟车模型（Carfollowingmodels）是运用动力学方法研究在无法超车的单车道上车辆列队行驶时后车跟随前车的行驶状态，并用数学形式表达同时加以分析阐明的一种微观模型。其主要目的是通过观察各个车辆逐一跟驶的方式来了解单车道交通流的特性。通过求解跟车方程，可以得到任意时刻车队中各车辆的速度、加速度和位置，用于分析车队的安全状况，在此基础上，提出改进车队安全的措施，如给驾驶人提供较多的信息、设法减少驾驶人的反应时间等。

运用跟车模型可以分析交通流稳定性，包括局部稳定性和渐进稳定性。对于稳定性的研究具有特殊意义，它有助于解释引起追尾事故和交通堵塞的原因，同时也可用于隧道等瓶颈路段车流特性的分析与改进。跟车模型在20世纪60年代就被用于评估驾驶人辅助系统、研究公共汽车车队特性等方面。当前在智能交通系统，如自动巡航系统的开发中，相关学者也对车辆的跟车模型进行了大量细致的研究，以保证自动控制下的车辆在跟随过程中能安全而平稳地行驶。

跟车模型的另一重要应用是交通仿真，在20世纪80年代后期以来所进行的跟车模型研究，基本上都是基于开发交通流仿真模型或是模拟驾驶。根据不同的开发目的，跟车模型各有特点，如专门用于城市道路交通仿真的跟车模型注重对城市交通中车辆反复停车一起步的模拟；基于自动巡航系统的仿真注重对，人机操作界面的模拟；对智能交通系统中的驾驶模拟则注重对驾驶人的信息接受与处理的模拟等。通过对各种交通流的仿真，可以进行交通改进措施、交通管制方案的评价以及道路通行能力研究和交通政策评价等方面的工作。

按照建模原理的不同，跟车模型可分为刺激—反应模型、安全距离模型、心理—生理模型和基于模糊逻辑的跟车模型四种主要模型。1

CHR模型建立刺激一反应模型的雏形最早由Reuschel和Pipes分别单独提出，其早期形式为假设驾驶人试图调节本车速度以与前车速度相一致。根据两个公认的假设：（1）驾驶人将考虑本车与前车的速度差调节车速；（2）驾驶人存在反应延迟，建立如下车辆行驶动力学方程：

an+1（t+T）=cΔvn,n+1（t）

其中，an+1（t+T）表示t+T时刻第n+1辆车（后车）的加速度，Δvn,n+1表示t 时刻第n辆车（前车）与第n+1辆车之间的速度差（相对速度），T为驾驶人的反应时间，c为待定比例参数。

20世纪50年代由通用汽车研究实验室的Chandler.Herman和Montroll对该模型进行了实验分析，测试8辆车跟随一辆“理想”速度变化（从15km/h～120km/h之间变化）的前导车的反应情况，车辆之间用金属线连接以测量车间距和相对速度，试验持续了30min。试验数据表明，加速度与速度差具有明显的相关性（r2>0.8），但待定比例参数c和反应时间T的变化幅度较大，变化区间分别为0.17～0.74s-1和1.0～2.2s，不能认定为常数。

Gazis、Herman和Rothery引入了“反应=灵敏度x刺激”的心理学公式，并对灵敏度项进行改进，增加了车间距和本车速度两个影响因素，构成如下非线性跟车模型（常被称为CHR模型）：

an+1（t+T）=cvmn+1（t+T）Δvn,n+1（t）/cΔxln,n+1（t）

其中，vn+1（t+T）表示t+T时刻第n+1辆车的速度，Δxn,n+1（t）表示t时刻第n辆车与第n+1辆车之间的距离，m、l为待定的幂次参数。

这个模型由于增加了车间距和本车速度两个因素，以及m、l两个待定的幂次参数，使得该模型更具有通用性，不仅能针对不同地区和驾驶环境下的驾驶行为进行建模，还可以通过选择m、l的不同组合区分加速、减速、刹车或者平稳驾驶等不同状态分别建模。随后有大量学者对该模型进行了研究，尝试标定m、I之间的最佳组合。
此外，一些学者也提出了其他形式的刺激一反应模型。一类是建模集中在模型右侧项的形式，如考虑速度差与车间距的线性加权组合形式、增加前后车当前时刻加速度的线性组合等。另一类是受Herman、Montroll和Potts提出的多辆前车思路的启发，即驾驶人不仅考虑正在跟随的那辆前车，而且通常同时考虑两辆以上的前车，从而建立各种形式的双前车跟车模型。

刺激一反应模型的一个重要特性是可以通过积分导出稳态交通流模型，在动态微观交通流模型和稳态宏观交通流模型之间建立了桥梁，从而在某种程度上印证了这些不同来源的理论的合理性。常见的稳态交通流模型和CHR模型中m、l取值的对应关系参见下表。

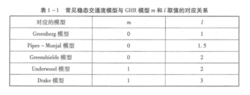
刺激一反应模型由于是最早的跟车模型而具有开创意义，之后提出的许多跟车模型都源于它所建立的刺激一反应基本关系。同时它形式简单、物理意义明确。但是随着对这一领域的深人研究，其模型对于复杂交通现象的描述还不能令人满意，因此还需进一步研究和改进。在交通仿真软件TransMod-eler及其前身MITSIM中跟随驾驶状态采用了改进的CHR模型。1

跟车理论的应用1）描述车流的稳定性，由反应时间、灵敏度、前后两车的车头间距及前车速度等已知条件，列出跟车模型方程并求解，分析计算结果，根据跟随车流的速度与车头间距的变化情况来描述车流的稳定性。

2）依据跟车理论可寻求车辆跟车运动的规律，估计车流中前、后车之间的相互影响。为了维持与行车速度相适应的车头间距，而不致过小，交通管理中可根据道路交通环境和气候条件，控制车流量不超过规定的交通量，避免因流量过大，后车紧迫前车，形成追随间隔缩小，造成一连串的尾撞事故的发生。在交通规划与交通管理中，可以此作为依据进行流量分配，使路网交通量的分布，不超过规定的交通量数值。

3）依据跟车理论，在道路交通管理中设法使前车给后车驾驶员提供较多的信息，如提供车头间距、相对速度等信息，以减少反应时间，帮助驾驶员跟随车辆安全行驶，防止尾撞事故的发生。

4）通过计算机模拟车队的跟车状态，研究车辆跟车运行中的安全性。若能将道路交通系统中的驾驶员反应时间、车头间距和相对速度的临界值三个参数减至最少，便可增强驾驶员的感觉，缩短驾驶员反应的延滞时间，以减少交通事故。

5）通过跟车理论可分析公共汽车的单车道流量。跟车试验的稳定性分析表明：所有的数据点都在渐近稳定区内，且验证了公共汽车跟车模型的预测；平均速度为53km/h，测出的公共汽车最大流量为1450veh/h。
通过跟车模型试验可预测小型汽车，驶入市区环路、干路的车流对市内交通的影响。

6）由跟车模型的一般形式，当参数m和l取各种不同的组合时，经积分确定边界条件，推导出各种不同的交通流模型。2

非线性跟车模型及其跟车模型的一般形式线性跟车模型的特点是简便和对稳定分析的敏感性，但它的明显缺点是跟随车的反应（加速度）仅为两车相对速度的函数，而与车辆的间距无关。

1959年，伽赛斯（Gazis）等人采用灵敏度系数与车头间距成反比的关系，得到了非线性跟车模型：

xˊˊn+1（t+T）=[a/[xn（t）-xn+1（t）]]·[xˊn（t）-xˊn+1（t）]

式中 a——比例常数，单位是距离/时间；

xi（t）——第i辆车在时刻t的位置。

根据伽赛斯的推导出——a=Vm=1/2Vf

由非线性跟车模型可以看出，灵敏度与交通流的临界车速成正比，与‘时刻两车间的距离成反比。这是符合实际情况的，因为车队的速度愈快，跟随车辆驾驶员的灵敏度也应愈高，否则车速高，制动距离长，易发生尾撞事故；而两车间的距离愈大，留给跟车驾驶反应、采取行动的时间愈长，即使驾驶员的灵敏率低些、反应时间长一点，也不会发生尾撞事故。

在1961年，伽赛斯又提出了跟车理论的一般形式

xˊˊn+1（t+T）=[axˊmn+1（t+T）/[xn（t）-xn+1（t）]l]·[xˊn（t）-xˊn+1（t）]

式中axˊmn+1（t+T）/[xn（t）-xn+1（t）]l为灵敏度；m，l为常数。

当m=0和l=0时，上述通式就成为线性模型公式；当m=0，l=1时，成为非线性模型公式。

跟车模型的一般形式还表明，灵敏度除了与交通流临界车速成正比，与两车间距离成反比之外，还与（t+T）时刻后车的速度成正比。因为后车的车速愈高，要求驾驶员的反应、敏捷水平也应愈高，否则会发生尾撞事故。3

本词条内容贡献者为:

杨明 - 副教授 - 西南大学