[科普中国]-超希腊-拉丁方

超希腊-拉丁方，即拉丁方阵（英语：Latin square），是一种 n × n 的方阵，在这种 n × n 的方阵里，恰有 n 种不同的元素，每一种不同的元素在同一行或同一列里只出现一次。

简介超希腊-拉丁方，即拉丁方阵（英语：Latin square），是一种 n × n 的方阵，在这种 n × n 的方阵里，恰有 n 种不同的元素，每一种不同的元素在同一行或同一列里只出现一次。

以下是两个拉丁方阵举例：

拉丁方阵有此名称是因为瑞士数学家和物理学家欧拉使用拉丁字母来做为拉丁方阵里的元素的符号。1

拉丁方阵的标准型当一个拉丁方阵的第一行与第一列的元素按顺序排列时，此为这个拉丁方阵的标准型，英语称为"reduced Latin square, normalized Latin square, 或Latin square in standard form"。1

同型类别参见：等价类和集合划分

许多对于拉丁方阵的运算都会产生新的拉丁方阵。例如说，交换拉丁方阵里的行、交换拉丁方阵里的列、或是交换拉丁方阵里的元素的符号，都会得到一个新的拉丁方阵。交换拉丁方阵里的行、交换拉丁方阵里的列、或是交换拉丁方阵里的元素的符号所得的新的拉丁方阵与原来的拉丁方阵称为同型(isotopic)。同型(isotopism)是一个等价关系，因此所有的拉丁方阵所成的集合可以分成同型类别(isotopic class)的子集合，同型的拉丁方阵属于同一个同型类别，而不属于同一个同型类别的拉丁方阵则不同型。1

正交拉丁方定理若n阶拉丁方存在r个两两正交的拉丁方，那么。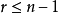

应用当该定理中的等号成立时，则该阶正交拉丁方族被称为完全的。 可以分析得到，当n为1时，只存在一个拉丁方，当n为2时，不存在正交拉丁方族。 此外，当n为6时，也不存在正交拉丁方族，这个结论是通过对三十六军官问题的尝试得到的。 三十六军官问题指的是是否有一个解决方案使得来自6个不同地区的6个不同军衔的军官排成6*6的方阵，其中每一行每一列的军官都来自于不同的地区且具有不同的军衔。 而该问题的方案即为6阶正交拉丁方的个数，该问题于1901年被Gaston Tarry证明为无解。 除了上述三种情况外，当阶数小于等于8时，均存在有n-1个正交的拉丁方。

如当n=3时，存在两个正交的拉丁方。

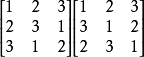当阶数更多时，可以通过正交拉丁方表得到正交拉丁方族。1

参见数独

吠陀方形‎‎

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学