[科普中国]-条件无偏估计

数学期望恰好等于被估计未知参数真值的估计量称为无偏估计量。若未知参数θ的估计量与给定的统计量满足期望之间的关系，则称估计量为参数θ关于统计量T1,T2,...,Tn的条件无偏估计量。

无偏估计数学期望恰好等于被估计未知参数真值的估计量称为无偏估计量。

无偏估计是用样本统计量来估计总体参数时的一种无偏推断。估计量的数学期望等于被估计参数的真实值，则称此此估计量为被估计参数的无偏估计，即具有无偏性，是一种用于评价估计量优良性的准则。无偏估计的意义是：在多次重复下，它们的平均数接近所估计的参数真值。无偏估计常被应用于测验分数统计中。

定义设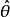为未知参数θ的估计量，T1,T2,...,Tn是给定的统计量，如果满足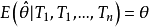则称其估计量为参数θ关于统计量T1,T2,...,Tn的条件无偏估计量。1

绝对无偏估计如果对于一切分布都满足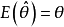，则称统计量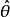为未知参数θ的绝对无偏估计量，

例如：修正样本方差是方差的绝对无偏估计。样本中位数，对于对称分布是中位数的无偏估计，但它不是中位数的绝对无偏估计。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学