在数学中,阿尔泽拉-阿斯科利定理是泛函分析中的一个定理,给出了一个从紧致度量空间射到度量空间的函数集合是否在关于一致收敛的拓扑意义上是紧集的充分必要条件。其中主要涉及的条件是函数集的等度连续性质。
简介等度连续的概念大约是在十九世纪的八十年代由两位意大利数学家阿斯科利(1883年-1884年)和阿尔泽拉(1882年-1883年)提出的。阿斯科利在1883年的论文中证明了定理中关于连续函数集成为紧集的充分条件的部分,而阿尔泽拉则在1895年的另一篇论文中证明了定理的另一部分:成为紧集的必要条件,并首次给出了定理的完整证明。而不久之后,在1906年,法国数学家弗雷歇又将这个定理进行了推广,使得在任意的能够定义极限的空间中都有同样的结果(比如度量空间或豪斯多夫空间)。
在阿尔泽拉-阿斯卡利定理被首次证明的年代,人们并没有充分理解该定理的重要意义。随着研究的不断深入,紧致性成为了分析学、拓扑学领域的关键概念,而此定理就描述了紧致性。该定理是利用欧拉法证明常微分方程组理论中的皮亚诺存在性定理时不可或缺的一环,也是复分析中的蒙泰尔定理的证明中的重要组成部分。此外,彼得-外尔定理的一个证明中用到了此定理。
预备概念以下是在定理的叙述和证明中将会用到的概念:
设K、X为两个度量空间。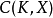 为从
为从 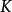 射到
射到 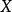 的连续映射的集合。此集合的一个子集被称为等度连续的,当且仅当对任意的x∈K和任意ε>0,存在x的邻域
的连续映射的集合。此集合的一个子集被称为等度连续的,当且仅当对任意的x∈K和任意ε>0,存在x的邻域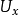 使得对所有的
使得对所有的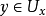 以及
以及 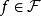 ,都有:
,都有:
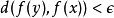 集合
集合 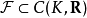 被称为逐点有界,如果对所有的
被称为逐点有界,如果对所有的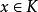 ,都有:
,都有:
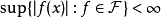 。
。
作为对比,一个集合 被称作一致有界,如果其中所有的函数的一致范数(绝对值的上确界)都小于某一个常数。
叙述实数域上的情况最简单的情况是在实数域上,这时的阿尔泽拉-阿斯科利定理的形式为:
考虑一个定义在实数轴中的有界闭区间 [a,b] 上的实数值函数序列 (fn)n∈N。如果这个序列是一致有界并且等度连续的,那么必定这个函数序列中存在一个子序列 (fnk) 是一致收敛的。
例子
设 (fn)n∈N是一个一致有界、可导,并且导数也是一致有界的函数序列,那么 (fn)n∈N这个序列满足阿尔泽拉-阿斯科利定理的条件,因为可以证明它也是等度连续的。因此,这个函数列拥有一个一致收敛的子序列。
紧度量空间和紧豪斯多夫空间对于一般的度量空间,阿尔泽拉-阿斯科利定理定义如下:
设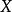 为一个紧度量空间,
为一个紧度量空间,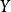 为一个完备的度量空间,那么
为一个完备的度量空间,那么 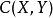 的子集
的子集 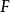 在紧致开拓扑中是紧致的当且仅当它是等度连续、完全有界的闭集。
在紧致开拓扑中是紧致的当且仅当它是等度连续、完全有界的闭集。
这里,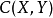 表示从
表示从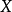 射到
射到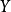 的连续函数的集合。而它的子集
的连续函数的集合。而它的子集 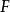 被称作完全有界当且仅当
被称作完全有界当且仅当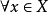 ,集合
,集合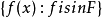 都是
都是 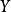 中相对紧致的子集。如果一个集合在紧致开拓扑中是紧致的,那么它之中的所有序列都拥有一个一致收敛到其中的子序列。
中相对紧致的子集。如果一个集合在紧致开拓扑中是紧致的,那么它之中的所有序列都拥有一个一致收敛到其中的子序列。
更广泛地,对于X是紧豪斯多夫空间的情况,定理一样成立:
设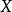 为一个紧豪斯多夫空间,那么
为一个紧豪斯多夫空间,那么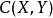 的子集
的子集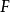 在紧致开拓扑中是紧致的当且仅当它是等度连续、完全有界的闭集。
在紧致开拓扑中是紧致的当且仅当它是等度连续、完全有界的闭集。
阿尔泽拉-阿斯科利定理是对于紧豪斯多夫空间上的连续函数的代数性质的研究中的一个重要结果。进一步的研究可以将上面的结果进行进一步的推广。比如说,函数的取值空间可以变为豪斯多夫的拓扑向量空间,这时仍然有基本相同的定理。
证明必要性该定理的必要性比较显然,实用价值也比较小。事实上,由紧度量空间X到完备的度量空间Y的任何一列连续映射序列{fn}如果在X上一致收敛,那么它收敛到一个连续映射f。由紧度量空间上连续映射f的一致连续性和收敛的一致性可以证明,该映射序列是等度连续的。同时由收敛的一致性和连续映射将紧集映为紧集的性质可以推出该序列完全有界。
若集合F中的映射不一致有界,则由定义,对任意n∈N,存在F中的映射fn,使得其范数大于n。{fn}的任意一个子列都不是完全有界的,故任意子列都非一致收敛,与假设矛盾。若集合F中的映射不等度连续,则存在ε>0,对任意的n∈N,存在x1、x2和某个集合中某个映射fn,满足d(x1,x2)0,存在δ,使得对任意x,y属于F,任意gn,只要d(x,y)Ni都有d(gm(ξi),gn(ξi))N,都有d(gm(ξk),gn(ξk))




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国