[科普中国]-并矢张量

在多重线性代数里，并矢张量(dyadic tensor)是一个以特别标记法写出的二阶张量，是由成对的向量并置形成的。针对这特别标记法，有一套专门计算这种表达式，类似于矩阵代数规则的方法。并矢张量的每一对向量的并置称为并矢(dyad)。两个单位基底向量的并矢积称为单位并矢(unit dyad)。标量与单位并矢的乘积就是并矢。

公式表达例如，设定两个三维向量和，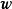

，

；

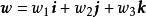其中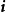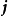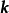，、、，形成了一个三维空间里的标准正交基的单位基底向量。

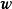那么，与并置成为

；

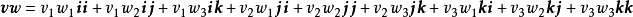其中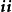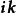，、、等等，都是单位并矢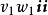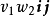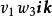，、、 等等，都是并矢。

并矢张量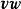也可以表达为

。

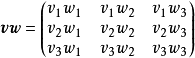定义根据Morse与feshbach所著作的教科书，在三维空间里，并矢张量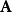是一个3×3阵列，其分量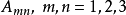，当从一个坐标系变换到另外一个坐标系时，遵守协变变换(covariant transformation)的定律。

；

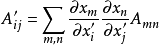其中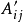，是变换后的分量。

所以，并矢张量是一个二阶协变张量。反过来说，按照这定义推广，任意二阶协变张量都是并矢张量：

。

并矢张量运算应用点积，并矢张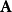量可以与向量综合在一起：

；

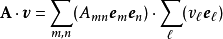其中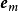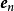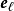，、、，都是标准正交基的基底向量。

注意到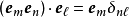；其中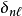，是克罗内克函数。所以，

；

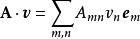这点积运算得到的结果是一个协变向量。

并矢张量的缩并(tensor contraction)运算，将每一个并置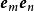，替换为两个单位基底向量的点积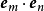，以方程式表达为

。

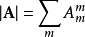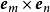只成立于三维空间，并矢张量的旋转因子运算，将每一个并置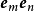，替换为两个单位基底向量的叉积，以方程式表达为

。

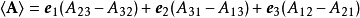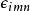这也可以表达为与列维-奇维塔符号的完全缩并：

。

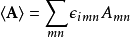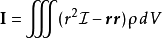
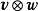
进阶理论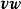两个向量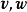的并矢积其实就是张量积。 两个并矢积作形式上的相加就是并矢张量，从而并矢张量和二阶张量（严格地说，是二阶的反变张量）是同义词。力学、电动力学中常见的例子就是单位并矢张量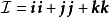、转动惯量以及马克士威应力张量等；量子力学中的角动量耦合(angular momentum coupling)理论也要用到并矢张量。

需要注意：并矢积是不可交换的，也就是说，除非两个矢量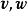线性相关，否则一定有。

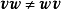在物理学中，并矢张量最重要的应用之一就是它和向量的缩并。对于并矢积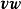和向量的缩并，规定

。

如果要求这种规定也适用于量子力学中的态矢量，在这种情况下就要特别注意每个式子右端各个向量的先后顺序：用狄拉克符号来写，则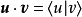。1

范例旋转设定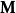为一个并矢张量：

。

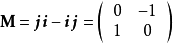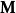是一个二维空间的 90°旋转算子(rotation operator) 。它可以从左边点积一个向量来产生一个旋转：

；

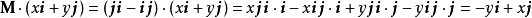或以矩阵表达，

。

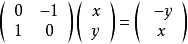一个一般的二维旋转并矢张量，会产生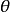角度反时针方向的旋转，表达为

；

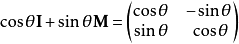其中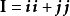，是二维的单位并矢张量。

量子力学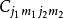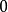设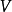是量子力学中所有的角动量本征态所张成的希尔伯特空间（囊括了所有可能的总角动量量子数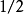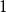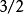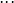，，，，），则。当我们要考虑角动量耦合的时候，就会遇到态矢量的并矢张量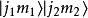，而且时常把它记作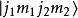或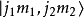等等。任取一些复数（但是其中只能有有限个非零），则

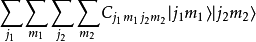
就是一个并矢张量。不妨把这个并矢张量记作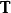，则它和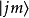的缩并就是

，

。

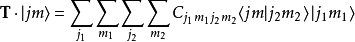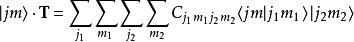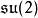
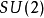在这其中，量子力学中最广为人知的就是通过CG矢量耦合系 数(Clebsch-Gordan coefficients) 所组合出来的张量。当然，在角动量耦合理论中，这样的张量被等同为某些角动量本征态，除了物理上的考虑之外，这更主要地还是有关李群及其李代数的表示的另外一个话题，请参看李群的表示(Lie group representation) 及李代数的表示(Lie algebra representation) ，在这里就不再深入探讨了。

实际上可以这样说，在量子力学中，只要物理问题涉及了系统的耦合，数学上就会导致态矢量的并矢。在这方面，还可以举一个常见的例子：由一维谐振子的态矢量所构成的并矢张量可以用来描述二维谐振子系统。

经典力学三维欧几里得空间上的并矢张量的例子非常多，例如转动惯量、应力张量、应变等等。这些例子实际上就是并矢张量这个概念的最初原型。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学