[科普中国]-最长路径问题-

最长路径问题是在给定图中找到最大长度的简单路径的问题。如果路径没有任何重复的顶点，则称为简单路径; 路径的长度可以通过其边数来测量，或者（在加权图中）通过其边缘的权重之和来测量。与可以在没有负权重循环的图中的多项式时间中求解的最短路径问题相比，最长路径问题是NP难的，这意味着除非P = NP，否则它不能在任意图的多项式时间内求解。还已知更强的硬度结果，表明难以近似。然而，它具有有向无环图的线性时间解，它在寻找调度问题的关键路径方面具有重要的应用。

NP-硬度可以使用哈密顿路径问题的减少来显示未加权最长路径问题的NP-硬度：当且仅当其最长路径具有长度n-1时，图G具有哈密顿路径，其中n是顶点的数量。 G.由于哈密顿路径问题是NP完全的，这种减少表明最长路径问题的决策版本也是NP完全的。在该决策问题中，输入是图G和数k;如果G包含k个或更多边的路径，则所需的输出为“是”，否则为无。

如果可以在多项式时间内解决最长路径问题，则可以通过找到最长路径然后将其长度与数字k进行比较来将其用于解决该决策问题。因此，最长的路径问题是NP难的。问题“在给定图中是否存在具有至少k个边的简单路径”是NP完全的。

在具有非负边缘权重的加权完整图中，加权最长路径问题与旅行推销员路径问题相同，因为最长路径总是包括所有顶点。

非循环图和关键路径在加权图G中两个给定顶点s和t之间的最长路径与通过将每个权重改变为其否定而从G导出的图-G中的最短路径相同。因此，如果在-G中找到最短路径，则在G中也可以找到最长路径1。

对于大多数图形，此变换无用，因为它在-G中创建负长度的循环。但是如果G是有向非循环图，则不能创建负循环，并且通过对-G中的最短路径应用线性时间算法，可以在线性时间中找到G中的最长路径，其也是有向无环图。例如，对于给定DAG中的每个顶点v，可以通过以下步骤获得以v结尾的最长路径的长度：

1、找到给定DAG的拓扑排序。

2、对于DAG的每个顶点v，在拓扑排序中，通过查看其传入的邻居并将这一个邻居记录的最大长度加1来计算以v结尾的最长路径的长度。如果v没有传入的邻居，则将以v结尾的最长路径的长度设置为零。在任何一种情况下，记录此数字，以便算法的后续步骤可以访问它。

完成此操作后，可以通过从具有最大记录值的顶点v开始，然后重复地向后踩到具有最大记录值的传入邻居，并反转在这条路。

用于调度一组活动的关键路径方法涉及构造有向无环图，其中顶点表示项目里程碑，边表示必须在一个里程碑之后和另一个里程碑之前执行的活动;通过估计相应活动将完成所花费的时间来对每个边缘进行加权。在这样的图表中，从第一个里程碑到最后一个里程碑的最长路径是关键路径，它描述了完成项目的总时间。

有向无环图的最长路径也可以应用于分层图绘制中：将有向非循环图G的每个顶点v分配给其数量是以v结尾的最长路径的长度的层，导致G的层分配最小可能的层数。

特殊类别的图表Dijkstra在20世纪60年代提出了一种用于在树中找到最长路径的线性时间算法，而该算法的形式证明于2002年出版。此外，最长路径可以在加权树上的多项式时间，块图，cacti，上的二分置换图，和托勒密图上计算。

对于区间图类，已知O（n4）时间算法，其使用动态编程方法。这种动态规划方法已被用于获得更大类圆弧图和共同可比性图（即可比性图的补充，也包含置换图）的多项式时间算法，两者具有相同的运行时间O（n 4）。后一种算法基于共同可比性图的词典深度优先搜索（LDFS）顶点排序的特殊属性。对于共同可比性图，还已知具有较高运行时间O（n7）的替代多项式时间算法，其基于由输入协同可比性图的补充定义的部分有序集的Hasse图。

此外，最长路径问题可以在具有有界树宽或有界团宽的任何类图的多项式时间内解决，例如距离-遗传图。最后，在哈密顿路径问题是NP难的所有图类上显然是NP难的，例如在分裂图，圆图和平面图上。

参数化复杂性当通过路径长度参数化时，最长路径问题是固定参数易处理的。例如，它可以通过执行以下步骤的算法在输入图形的大小上按时间线性求解（但在路径长度上呈指数）：

执行图表的深度优先搜索。设d是得到的深度优先搜索树的深度。

使用深度优先搜索树的根到叶路径的顺序，按照搜索遍历的顺序，构建图的路径分解，路径宽度为d。

将动态编程应用于此路径分解以找到时间上最长的路径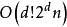，其中n是图中顶点的数量。

由于输出路径的长度至少与d一样大，因此运行时间也受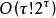的限制，其中l是最长路径的长度。使用颜色编码，可以将对路径长度的依赖性降低到单指数。类似的动态编程技术表明，当通过图的树宽参数化时，最长路径问题也是固定参数易处理的。

对于有界集团宽度的图，最长路径也可以通过多项式时间动态规划算法求解。但是，多项式的指数取决于图的clique-width，因此该算法不是固定参数易处理的。由clique-width参数化的最长路径问题对于参数化复杂度类W 来说很难，表明固定参数易处理算法不太可能存在。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学